Тождества

Главная Алгебра

Скачать презентацию (0.39 мб)

Слайды и текст этой презентации

Слайд №1
	ТОЖДЕСТВА 7 класс

Слайд №2
	Презентация составлена учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной
Слайд №3
	Математика нужнаБез нее никак нельзяУчим, учим мы, друзья, Что же помним мы с утра?
Слайд №4
	Решить уравнение (по вариантам) 1) (2х + 1)? = 13 + 4х? 2) (3х — 1)? — 9х? = — 35
Слайд №5
	Проверьте решение: решение 4х? + 4х + 1 = 13 + 4х? 4х? + 4х — 4х? = — 1 + 13 4х = 12 х = 3 Ответ: 3 2) решение 9х? — 6х + 1 — 9х? = -35 -6х = — 1 – 35 — 6х = — 36 х = 6 Ответ: 6
Слайд №6
	Задание: Выполнить действия(по вариантам)
Слайд №7
	Решение:
Слайд №8
	В теорию: Определение ТОЖДЕСТВОМ НАЗЫВАЕТСЯ РАВЕНСТВО, ВЕРНОЕ ПРИ ЛЮБЫХ ДОПУСТИМЫХ ЗНАЧЕНИЯХ ПЕРЕМЕННЫХ. 13.06.2014 8 http://aida.ucoz.ru
Слайд №9
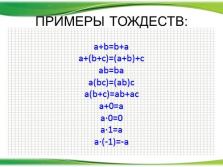	ПРИМЕРЫ ТОЖДЕСТВ: a+b=b+a a+(b+c)=(a+b)+c ab=ba a(bc)=(ab)c a(b+c)=ab+ac a+0=a a?0=0 a?1=a a?(-1)=-a
Слайд №10
	Запомним: ВЫРАЖЕНИЯ, СООТВЕТСВЕННЫЕ ЗНАЧЕНИЯ КОТОРЫХ РАВНЫ ПРИ ЛЮБЫХ ДОПУСТИМЫХ ЗНАЧЕНИЯХ ПЕРЕМЕННЫХ, НАЗЫВАЮТСЯ ТОЖДЕСТВЕННО РАВНЫМИ. (a?)? и a6 ab?(-a?b) и –a?b? ЗАМЕНУ ОДНОГО ВЫРАЖЕНИЯ ДРУГИМ, ТОЖДЕСТВЕННО РАВНЫМ ЕМУ, НАЗЫВАЮТ ТОЖДЕСТВЕННЫМ ПРЕОБРАЗОВАНИЕМ
Слайд №11
	В теорию: Способы доказательства тождеств: Преобразование левой части тождества так, чтобы получилась её правая часть (если после преобразования левой части, выражение получится как в правой части , то данное выражение является тождеством)
Слайд №12
	Проверьте, данное выражение – тождество?
Слайд №13
	Решение: Преобразуем левую часть равенства: а(в — х) + х(а + в) = = ав – ах + ах + хв = = ав + хв = в(а + х)
Слайд №14
	Вывод: В результате тождественного преобразования левой части равенства, мы получили его правую часть и тем самым доказали, что данное равенство является тождеством.
Слайд №15
	В теорию (способы доказательства тождеств): 2. Преобразование правой части тождества так, чтобы получилась её левая часть
Слайд №16
	Проверьте, данное выражение – тождество?
Слайд №17
	Решение: Преобразуем правую часть равенства (а+2)(а+5)= = а? + 5а + 2а+ + 10 = = а? + 7а + 10
Слайд №18
	Вывод: В результате тождественного преобразования правой части равенства, мы получили его левую часть и тем самым доказали, что данное равенство является тождеством.
Слайд №19
	В теорию (способы доказательства тождеств): Преобразование обеих частей тождества…..(должны получится одинаковые выражения)
Слайд №20
	Докажите тождество:
Слайд №21
	Решение: Упростим обе части равенства
Слайд №22
	Вывод: Так как левая и правая части данного равенства равны одному и тому же выражению, то они тождественно равны между собой. Значит исходное равенство – тождество.
Слайд №23
	В теорию (способы доказательства тождеств): 4. Найти разность между правой и левой частями выражения. (если эта разность равна нулю, то данное выражение — тождество)
Слайд №24
	Докажите тождество: (m-a)(m-b) = m?- (a+b)m + ab
Слайд №25
	Решение:(найдем разность между левой и правой частями выражения) (m-a)(m-b) – [m? — (a+b)m + ab] = =m? — mb – ma + ab — [m? — am – bm + ab ] = = m? — mb – ma + ab — m? + am + bm — ab = = 0
Слайд №26
	Вывод: Так как разность между левой и правой частями выражения равна нулю, то данное выражения является тождеством
Слайд №27
	Работаем по учебнику: стр. 157 № 36.7 (а;б) № 36.6 (а;б)
Слайд №28
	Подведем итоги: Что такое ТОЖДЕСТВО? Какие существуют способы доказательства тождеств?
Слайд №29
	Спасибо за урок!