Числовые последовательности
Слайды и текст этой презентации
| Слайд №1 | |
 |
Числовые последовательности Способы задания последовательностей |
| Слайд №2 | |
 |
Дни недели Названия месяцев Классы в школе Номер счёта в банке Дома на улице Последовательности составляюттакие элементы природы, которые можно пронумеровать |
| Слайд №3 | |
 |
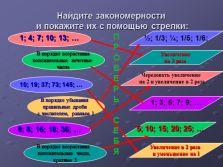Найдите закономерности и покажите их с помощью стрелки: 1; 4; 7; 10; 13; … В порядке возрастания положительные нечетные числа 10; 19; 37; 73; 145; … В порядке убывания
6; 8; 16; 18; 36; … Чередовать увеличение
1; 3; 5; 7; 9; … П С |
| Слайд №4 | |
 |
Рассмотренные числовые ряды – примеры числовых последовательностей Обозначают члены последовательности так а1; а2; а3; а4; … аn |
| Слайд №5 | |
 |
Способы задания последовательностей 1. Описанием 2. Формулой общего члена 3. Рекуррентный 4.Таблицей |
| Слайд №6 | |
 |
Задание последовательности описанием Пример: Составить последовательность, в которой на четных местах 0, на нечетных местах – 1. Получим последовательность: |
| Слайд №7 | |
 |
Задание последовательности формулой 1) an= 3*n +2, a5 = 3*5+2 17 a10 = ? 32 a100 = ? 302 2) an= 3+n , a5 = ? 8 a10 = ? 13 a100 = ? 103 3) an= n2+1, a5 = ? 26 a10 = ? 101 a100 = ? 10001 4) an= 2n-1 , a5 = ? 16 a7 = ? 64 a10 = ? 512 08.03.2014 22:35 Замечание Числовые последовательности являются частным случаем функций с натуральным аргументом. |
| Слайд №8 | |
 |
Рекуррентный способ задания последовательности Название способа произошло от слова «recurro» — возвращаться. Рекуррентной называется формула, выражающая любой член последовательности, начиная с некоторого через предыдущие. Например: an+1= 3+n можно задать: а1 =4, an+1 = an +1 a2= a1 +1= 4+1=5, a3= a2 +1= 5+1=6,… 08.03.2014 22:35 |
| Слайд №9 | |
 |
Табличный способ 08.03.2014 22:35 |
| Слайд №10 | |
 |
Бесконечные последовательности: (an) 1, 3, 5, 7, 9, 11,… — последовательность нечетных чисел (возрастающая) (an) -5, -10, -15, -20, -25, … — последовательность отрицательных чисел, кратных 5 (убывающая) Конечные последовательности: (an) 1, 2, 3, 4, 5, 6, 7, 8, 9 — последовательность однозначных натуральных чисел. (an) 10,20,30,40,50,60,70,80,90 – последовательность двузначных чисел, кратных 10. 08.03.2014 22:35 Примеры последовательностей |
| Слайд №11 | |
 |
Последовательности заданы формулами: an=(-1)nn2 an=n4 an=n+4 an=-n-2 an=2n-5 an=3n-1 2. Укажите, какими числами являются члены этих последовательностей Положительные и Положительные Отрицательные отрицательные Выполните следующие задания: Впишите пропущенные члены последовательности: 1; ___; 81; ___; 625; … 5; ___; ___; ___; 9; … ___; ___; 3; 11; ___; -1; 4; ___; ___; -25; … ___; -4 ; ___; ___; -7; … 2; 8; ___; ___; ___; … -9 16 -3 -5 -6 26 80 242 СЕБЯ |
| Слайд №12 | |
 |
Числа Фибоначчи х1 =х2=1; хn+2=xn+1 +xn; n=1; 2; 3; … Последовательность чисел Фибоначчи задается так: Вычислим несколько её первых членов: 1; 1; 2; 3; 5; 8; 13; 21; 34;55; 89; 144; 233; 377; … Треугольник Паскаля Бесконечная числовая таблица треугольной формы, 1 |
| Слайд №13 | |
 |
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 Связь между числами Фибоначчи и треугольником Паскаля Между числами Фибоначчи и треугольником Паскаля существует связь. Подсчитаем для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел, получим: Для 1 диагонали – 1; Для 2 диагонали – 1; Для 3 диагонали – 1+1=2; Для 4 диагонали – 1+2=3; Для 5 диагонали – 1+3+1=5; Для 6 диагонали – 1+4+3=8 … В результате мы получаем числа Фибоначчи: 1; 1; 2; 3; 5; 8; … Всегда сумма чисел n-ой диагонали есть n-ое число Фибоначчи. |
| Слайд №14 | |
 |
Последовательности составляют такие элементы природы, которые можно пронумеровать 08.03.2014 22:35 a1 a2 a3 a4 b3 b2 b1 a1 a2 a3 a4 a5 |
