Метод математической индукции

Главная Алгебра

Скачать презентацию (0.48 мб)

Слайды и текст этой презентации

Слайд №1
	Презентация по математике на тему: «Метод математической индукции» Выполнила Кондратьева Анастасия 10 класс

Слайд №2
	В основе математического исследования лежит Дедуктивный метод Индуктивный метод
Слайд №3
	Дедуктивный метод Дедуктивный метод – это рассуждение, исходным моментом которого является общее утверждение, а заключительным – частный результат.
Слайд №4
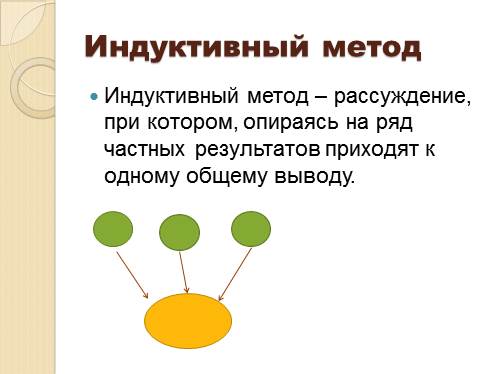
	Индуктивный метод Индуктивный метод – рассуждение, при котором, опираясь на ряд частных результатов приходят к одному общему выводу.
Слайд №5
	Пример рассуждения по индукции Требуется установить, что каждое четное число в пределах от 4 до 100 можно представить в виде суммы двух простых чисел. Для этого переберем все интересующие нас числа и выпишем соответствующие суммы:
Слайд №6
	4=2+2; 6=3+3; 8=3+5; 10=5+5; …; 92=3+89; 94=5+89; 96=7+89; 98=9+89; 100=3+97. Эти 49 равенств (мы выписали только 9 из них) показывают, что утверждение о том, что любое четное число от 4 до100 можно представить в виде суммы двух простых чисел, верно и было доказано путем перебора всех частных случаев.
Слайд №7
	Это был пример полной индукции, когда общее утверждение доказывается для конечного множества элементов при рассмотрении каждого из этих элементов. Но чаще общее утверждение относится не к конечному, а к бесконечному множеству. В таких случаях общее утверждение может быть угаданным, полученным неполной индукцией. Оно может оказаться верным или неверным.
Слайд №8
	Пример 1 Выдвинем гипотезу, что сумма первых n нечетных чисел равна n2. Рассмотрим на примерах:1=12 ; 1+3=4=22 ; …; 1+3+5+7+9+11=36=62 Гипотеза подтвердилась, однако она останется гипотезой, пока не будет доказана. Доказательство: 1+2+5+…+(2n-1) – сумма n членов арифметической прогрессии, значит, Sn= ???? 1 + ???? ???? 2 ?????= 1+(2?????1) 2 ?n= ???? 2
Слайд №9
	Пример 2 Рассмотрим последовательность ???? ???? = ???? 2 +n+17. Выпишем первые четыре члена: у 1 =19; y2 =23; y3 = 29; y4 = 37. Возникает гипотеза, что вся последовательность состоит из простых чисел. Однако это не так: У16 =162 +16 +17=16(16+1)+17= 17(16+1)= 17?17. Это составное число.
Слайд №10
	Итак, неполная индукция не считается в математике методом строгого доказательства, т.к. может привести к ошибке. Во многих случаях, когда доказательство найти трудно, обращаются к особому методу рассуждений, который называется методом математической индукции.
Слайд №11
	Метод математической индукции Суть метода можно разъяснить на примере. Рассмотрим арифметическую прогрессию а1 , а2 , а3 , … аn , … . По определению ???? ????+1 = ???? ???? +????, значит, ???? 1 = ???? 1 ; ???? 2 = ???? 1 +d; ???? 3 = ???? 2 +d= ???? 1 +2d;и т.д.
Слайд №12
	Нетрудно догадаться, что для любого номера n справедливо равенство ???? ???? = ???? 1 + ?????1 ???? Утверждение выведено нами интуитивно, попробуем обосновать его. Если n=1, то а1= а1 + (1-1)d – верное равенство, то есть утверждение для n=1 верно. Предположим, что утверждение верно для натурального числа n=k, т.е. предположим, что ak= а1+(k-1)d. И попробуем доказать, что утверждение верно для n=k+1, т.е. ak+1=а1+kd В самом деле по определению арифметической прогрессии ak+1=ak+d= (а1+(k-1)d)+d= а1+kd
Слайд №13
	Для n=1 утверждение ???? ???? = ???? 1 + ?????1 ???? верно. Мы оказали, что если для n=k эта формула верна, то и для n=k+1 формула тоже верна. Но т.к. формула верна для n=1, то она верна и для n=2, а значит и для n=3 и т.д. т.е формула верна для любого натурального числа n. Утверждение доказано.
Слайд №14
	Составляющие метода математической индукции Пусть нужно доказать справедливость А(n), где n – любое натуральное число. Для этого сначала проверим справедливость А(n) для n=1(базис математической индукции). Затем докажем, что для любого натурального числа k справедливо следующее: если А(k) – справедливо, то А(k+1), тоже справедливо(индукционный шаг). Делаем вывод, что А(n) справедливо для любого n.
Слайд №15
	Принцип математической индукции: Утверждение, зависящее от натурального числа n, справедливо для любого n, если выполнены следующие условия: А)утверждение верно для n=1; Б)из справедливости утверждения для n=k, где k – любое натуральное число, вытекает справедливость утверждения и для следующего натурального числа n=k+1