Правильные Многогранники
Скачать презентацию (1.3 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Правильные Многогранники |
| Слайд №2 | |
 |
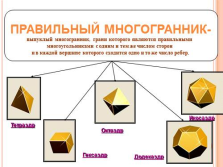ПРАВИЛЬНЫЙ МНОГОГРАННИК- Гексаэдр |
| Слайд №3 | |
 |
«эдра» — грань
«тетра» — 4 «гекса» — 6 «окта» — 8 «икоса» — 20 «додека» — 12 |
| Слайд №4 | |
 |
Тетраэдр – представитель правильных выпуклых многогранников. Поверхность тетраэдра состоит из четырех равносторонних треугольников, сходящихся в каждой вершине по три. ТЕТРАЭДР |
| Слайд №5 | |
 |
Куб или гексаэдр – представитель правильных выпуклых многогранников. Куб имеет шесть квадратных граней, сходящихся в каждой вершине по три. КУБ (ГЕКСАЭДР) |
| Слайд №6 | |
 |
Октаэдр – представитель семейства правильных выпуклых многогранников. Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине по четыре. ОКТАЭДР |
| Слайд №7 | |
 |
Додекаэдр – представитель семейства правильных выпуклых многогранников. Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по три. ДОДЕКАЭДР |
| Слайд №8 | |
 |
Икосаэдр – представитель семейства правильных выпуклых многогранников. Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в каждой вершине по пять. ИКОСАЭДР |
| Слайд №9 | |
 |
|
| Слайд №10 | |
 |
Симметрия в пространстве В стереометрии рассматривают симметрию относительно точки, прямой и плоскости. Точка(прямая,плоскость)называется центром(осью,плоскостью) симметрии фигуры,если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры Центр симметрии Ось симметрии Плоскость симметрии |
| Слайд №11 | |
 |
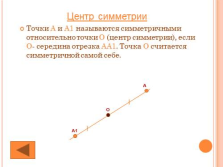Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О- середина отрезка АА1. Точка О считается симметричной самой себе. Центр симметрии А |
| Слайд №12 | |
 |
Ось симметрии Точки А и А1 называются симметричными относительно прямой а(ось симметрии), если прямая а проходит через середину отрезка АА1 и перпендикулярна к этому. Каждая точка прямой а считается симметричной самой себе. А а А1 |
| Слайд №13 | |
 |
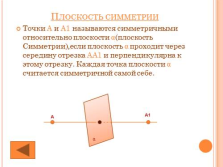Плоскость симметрии Точки А и А1 называются симметричными относительно плоскости ?(плоскость Симметрии),если плоскость ? проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости ? считается симметричной самой себе. ? А А1 |
| Слайд №14 | |
 |
Симметрию можно встретить в… природе архитектуре технике быту |
| Слайд №15 | |
 |
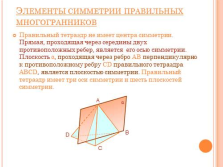Элементы симметрии правильных многогранников Правильный тетраэдр не имеет центра симметрии. Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость ?, проходящая через ребро АВ перпендикулярно к противоположному ребру CD правильного тетраэдра ABCD, является плоскостью симметрии. Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии. |
| Слайд №16 | |
 |
Элементы симметрии правильных многогранников Куб имеет один центр симметрии- точку пересечения его диагоналей. Прямые a и b, проходящие соответственно через центры противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. Все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии. |
| Слайд №17 | |
 |
Элементы симметрии правильных многогранников Правильный октаэдр(1), правильный икосаэдр(2) и правильный додекаэдр(3) имеют центр симметрии и несколько осей и плоскостей симметрии. 1 2 3 |
Похожие записи:
