Решение задача по теме "Параллелограмм"
Скачать презентацию (0.13 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Четырехугольники 8 классгеометрия Урок № 3 Параллелограмм. Решение задач 03.12.2012 1 www.konspekturoka.ru Закрепить знания о свойствах и признаках параллелограмма в процессе решения задач |
| Слайд №2 | |
 |
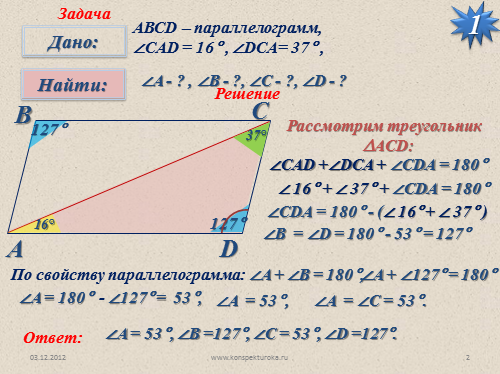
03.12.2012 www.konspekturoka.ru 2 1 АВСD – параллелограмм, ?CAD = 16° , ?DCA= 37° , ?A — ? , ?B — ?, ?C — ?, ?D — ? Задача Решение Рассмотрим треугольник ?ACD: ?CAD +?DCA + ?СDА = 180° ? 16° + ? 37° + ?СDА = 180° ?СDА = 180° — (? 16° + ? 37° ) ?B = ?D = 180° — 53° = 127° По свойству параллелограмма: ?A + ?B = 180°, ?A + ?127° = 180° ?A = 180° — ?127° = 53°, ?A = 53°, ?A = ?C = 53°. Ответ: ?A = 53°, ?B =127°, ?C = 53°, ?D =127°. |
| Слайд №3 | |
 |
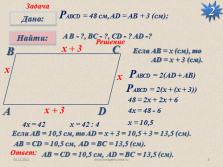
03.12.2012 www.konspekturoka.ru 3 2 РАВСD = 48 см, AD = AB + 3 (см); A B — ?, ВC — ?, CD — ? AD -? Задача Ответ: Решение х х х + 3 х + 3 Если АВ = х (см), то AD = x + 3 (см). РАВСD = 2(AD + AB) РАВСD = 2(x + (x + 3)) 48 = 2x + 2x + 6 4x = 48 — 6 4x = 42 x = 42 : 4 x = 10,5 Если АВ = 10,5 см, то AD = x + 3 = 10,5 + 3 = 13,5 (см). АВ = CD = 10,5 см, AD = BC = 13,5 (см). АВ = CD = 10,5 см, AD = BC = 13,5 (см). |
| Слайд №4 | |
 |
03.12.2012 www.konspekturoka.ru 4 3 РАВСD = 48 см, AD — AB = 7 (см); A B — ?, ВC — ?, CD — ? AD -? Задача Ответ: Решение х х х + 7 х + 7 Если АВ = х (см), то AD = x + 7 (см). РАВСD = 2(AD + AB) РАВСD = 2(x + (x + 7)) 48 = 2x + 2x + 14 4x = 48 — 14 4x = 34 x = 34 : 4 x = 8,5 Если АВ = 8,5 см, то AD = x + 7 = 8,5 + 7 = 15,5 (см). АВ = CD = 8,5 см, AD = BC = 15,5 (см). АВ = CD = 8,5 см, AD = BC = 15,5 (см). |
| Слайд №5 | |
 |
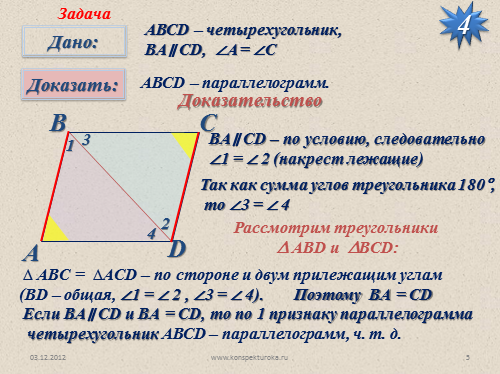
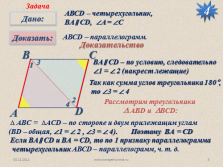
03.12.2012 www.konspekturoka.ru 5 4 АВСD – четырехугольник, BА? CD, ?A = ?C АВСD – параллелограмм. Доказательство Задача 1 2 3 4 BА? CD – по условию, следовательно ?1 = ? 2 (накрест лежащие) Рассмотрим треугольники ? АBD и ?BCD: Так как сумма углов треугольника 180°, то ?3 = ? 4 ? АBC = ?ACD – по стороне и двум прилежащим углам (ВD – общая, ?1 = ? 2 , ?3 = ? 4). Поэтому BА = CD Если BА? CD и BА = CD, то по 1 признаку параллелограмма четырехугольник АВСD – параллелограмм, ч. т. д. |
| Слайд №6 | |
 |
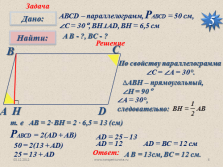
03.12.2012 www.konspekturoka.ru 6 5 Задача АВСD – параллелограмм, РАВСD = 50 см, ?С = 30°, BH?AD, BH = 6,5 см A B — ?, ВC — ? Решение Н ? По свойству параллелограмма ?С = ?А = 30°. ?АВН – прямоугольный, ?Н = 90° ?А = 30°, следовательно: т. е АВ = 2· ВН = 2 · 6,5 = 13 (см) РАВСD = 2(AD + AB) 50 = 2(13 + AD) 25 = 13 + AD AD = 25 – 13 AD = 12 Ответ: A B = 13см, ВC = 12 см. AD = ВС = 12 см |
| Слайд №7 | |
 |
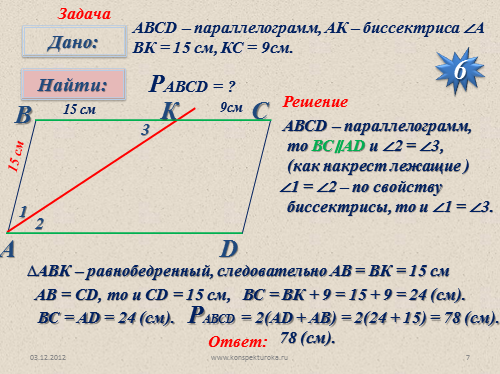
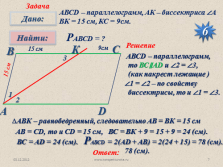
03.12.2012 www.konspekturoka.ru 7 Задача 6 АВСD – параллелограмм, АК – биссектриса ?А ВК = 15 см, КС = 9см. РАВСD = ? 1 2 3 Решение АВСD – параллелограмм, то ВС?AD и ?2 = ?3, (как накрест лежащие ) ?1 = ?2 – по свойству биссектрисы, то и ?1 = ?3. К ?АВК – равнобедренный, следовательно АВ = ВК = 15 см 15 см 9см АВ = СD, то и СD = 15 см, ВС = ВК + 9 = 15 + 9 = 24 (см). 15 см ВС = AD = 24 (см). РАВСD = 2(AD + AB) = 2(24 + 15) = 78 (cм). Ответ: 78 (cм). |
| Слайд №8 | |
 |
03.12.2012 8 Ответить на вопросы: www.konspekturoka.ru Спасибо за внимание! Какая фигура называется параллелограммом? Докажите, что в параллелограмме противоположные стороны и углы равны. Докажите, что в параллелограмме диагонали точкой пересечения делятся пополам. Сформулируйте и докажите признаки параллелограмма. |
