Кодирование вещественных чисел

Главная Информатика

Скачать презентацию (0.09 мб)

Слайды и текст этой презентации

Слайд №1
	Кодирование вещественных чисел Составила Соколова Е.В. Учитель информатики МБОУ СОШ № 1 г.Зубцов Тверская обл.

Слайд №2
	Для представления вещественных чисел (конечных и бесконечных десятичных дробей) используют формат с плавающей точкой (запятой). Форма с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком: R = m * рn m – мантисса, n – порядок, p – основание системы 11.06.2014 2 Кодирование вещественных чисел
Слайд №3
	Например, число 35,324 можно записать в таком виде: 0.35324х102 Здесь m=0.35324 — мантисса, n=2 — порядок Порядок указывает, на какое количество позиций и в каком направлении должна «переплыть», т.е. сместиться десятичная точка в мантиссе. Отсюда название «плавающая точка». Однако справедливы и следующие равенства: 35,324 = 3,5324101 = 0,0035324104 = 3532,4*102 и т.п. 11.06.2014 3 Кодирование вещественных чисел
Слайд №4
	Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа в форме с плавающей точкой 11.06.2014 4 Кодирование вещественных чисел
Слайд №5
	Мантисса в нормализованном представлении должна удовлетворять условию: 0,1p ? m < 1p Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. Значит для рассмотренного числа нормализованным представлением будет: 35,324=0.35324 * 102 11.06.2014 5 Кодирование вещественных чисел
Слайд №6
	± 1 б а й т 2 б м а й а т н 3 т б а и й т с с а 4 б а й т Машинный порядок Пусть в памяти компьютера вещественное число представляется в форме с плавающей точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы. Вот как эта информация располагается в ячейке: 11.06.2014 6 Кодирование вещественных чисел
Слайд №7
	Машинныйпорядок В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус Оставшиеся 7 бит первого байта содержат машинный порядок В следующих трех байтах хранятся значащие цифры мантиссы ± 1 б а й т 2 б м а й а т н 3 т б а и й т с с а 4 б а й т 11.06.2014 7 Кодирование вещественных чисел
Слайд №8
	Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. В десятичной системе это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка. 11.06.2014 8 Кодирование вещественных чисел
Слайд №9
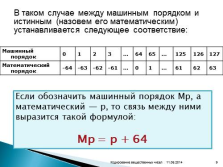	В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие: Машинный порядок 0 1 2 3 … 64 65 … 125 126 127 Математический порядок -64 -63 -62 -61 … 0 1 … 61 62 63 Если обозначить машинный порядок Мр, а математический — р, то связь между ними выразится такой формулой: Мр = р + 64 11.06.2014 9 Кодирование вещественных чисел
Слайд №10
	Итак, машинный порядок смещён относительно математического на 64 единицы и имеет только положительные значения. При выполнении вычислений с плавающей точкой процессор это смещение учитывает В двоичной системе счисления смещение: Мр2 = р2+100 00002 11.06.2014 10 Кодирование вещественных чисел
Слайд №11
	Теперь мы можем записать внутреннее представление числа 35,324 в форме с плавающей точкой 1) Переведем его в двоичную систему счисления с 24 значащими цифрами 35,324= 100011,0101001011110001102 11.06.2014 11 Кодирование вещественных чисел
Слайд №12
	2) Запишем в форме нормализованного двоичного числа с плавающей точкой: 0,100011010100101111000110*10110 Здесь мантисса, основание системы счисления (210=102) и порядок (610=1102)записаны в двоичной системе 11.06.2014 12 Кодирование вещественных чисел
Слайд №13
	3) Вычислим машинный порядок Мр2 = 110 + 100 0000 = 100 0110 4) Запишем представление числа в ячейке памяти порядок мантисса Знак числа 11.06.2014 13 Кодирование вещественных чисел
Слайд №14
	Число в форме с плавающей точкой занимает в памяти компьютера 4 байта (число обычной точности) или 8 байт (число двойной точности). Мы рассмотрели пример представления числа 35,324 обычной точности 11.06.2014 14 Кодирование вещественных чисел
Слайд №15
	Для того, чтобы получить внутреннее представление отрицательного числа -35,324, достаточно в полученном выше коде заменить в разряде знака числа 0 на 1 11.06.2014 15 Кодирование вещественных чисел
Слайд №16
	Представьте двоичное число -100,12 в четырёхбайтовом формате. Представьте число сначала в форме с плавающей запятой. Задание: 11.06.2014 16 Кодирование вещественных чисел
Слайд №17
	-100,12= -0,1001*211 Мантисса -0,1001 Порядок 11 Машинный порядок 11+100 0000=1000011 Решение: 11.06.2014 17 Кодирование вещественных чисел
Слайд №18
	Задания для самостоятельного выполнения Сравните числа: а) 318,4785?109 и 3,184785?1011 б) 218,4785?10-3 и 1847,85?10-4 2. Запишите числа в естественной форме: а) 0,1100000?2100 б) 0,1001111?2111 11.06.2014 18 Кодирование вещественных чисел