Логические выражение. Таблицы истинности. Логические схемы.
Скачать презентацию (0.28 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Обобщающий урок по теме:«ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ,ТАБЛИЦЫ ИСТИННОСТИ,ЛОГИЧЕСКИЕ СХЕМЫ» 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 Искандарова А.Р. г. Уфа |
| Слайд №2 | |
 |
Вопросы для повторения Что понимают под высказыванием? Высказывание(суждение) – это повествовательное предложение, в котором что-либо утверждается или отрицается. Высказывание может быть либо истинно, либо ложно. Привести примеры простых высказываний. Кошка является домашним животным. Процессор – это устройство обработки информации. Привести примеры сложных высказываний. Петя и Вася играют в шахматы. Принтер является устройством вывода информации или сканер устройством ввода информации. 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 |
| Слайд №3 | |
 |
Вопросы для повторения Что понимают под логическим выражением? Логическая формула (логическая выражение) – формула, содержащая лишь логические переменные и знаки логических операций. Какие значения могут принимать логические переменные? Логические переменные могут принимать лишь два значения: «истина» (1) и «ложь» (0). Назовите основные логические операции. Конъюнкция, дизъюнкция, отрицание. Каков порядок выполнения логических операций? Отрицание, конъюнкция, дизъюнкция. 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 |
| Слайд №4 | |
 |
Таблицы истинности Найдите значение выражений: 1 and (0 or not 0)= not(0 or 1) and 1= 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 |
| Слайд №5 | |
 |
Таблицы истинности Найдите значение выражений: 1 and (0 or not 0)=1*(0+1)=1 not(0 or 1) and 1=0*1=0 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 |
| Слайд №6 | |
 |
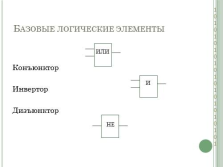Базовые логические элементы
Конъюнктор Инвертор Дизъюнктор |
| Слайд №7 | |
 |
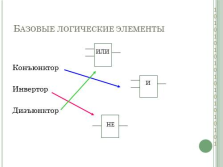Базовые логические элементы
Конъюнктор Инвертор Дизъюнктор |
| Слайд №8 | |
 |
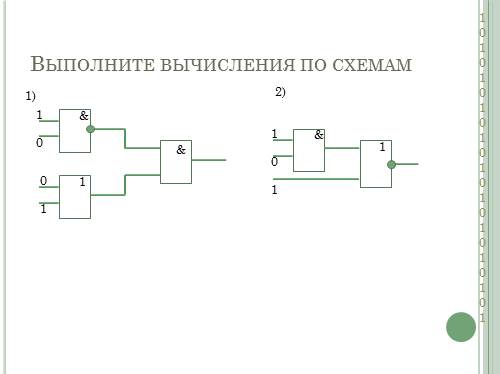
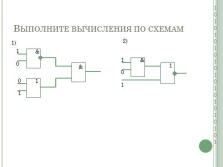
1 Выполните вычисления по схемам 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 & 1 0 1 0 1 & & 1 0 1 1 1) 2) |
| Слайд №9 | |
 |
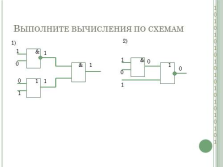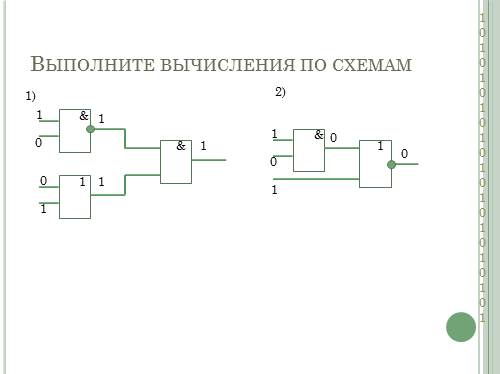
Выполните вычисления по схемам 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 & 1 0 1 0 1 & & 1 0 1 1 1) 2) 0 1 1 1 0 |
| Слайд №10 | |
 |
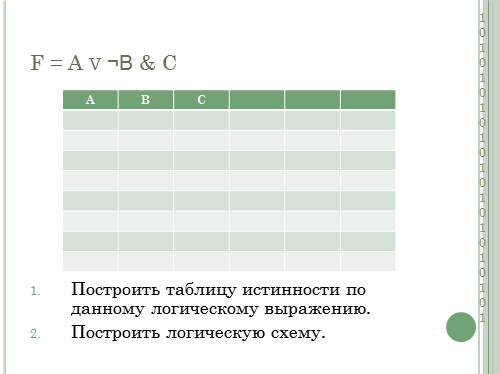
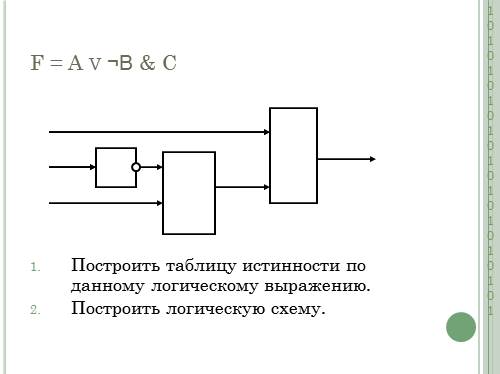
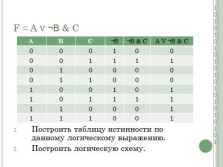
F = A v ¬В & С
Построить таблицу истинности по данному логическому выражению. |
| Слайд №11 | |
 |
F = A v ¬В & С
Построить таблицу истинности по данному логическому выражению. |
| Слайд №12 | |
 |
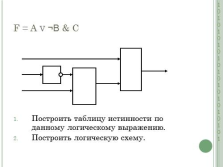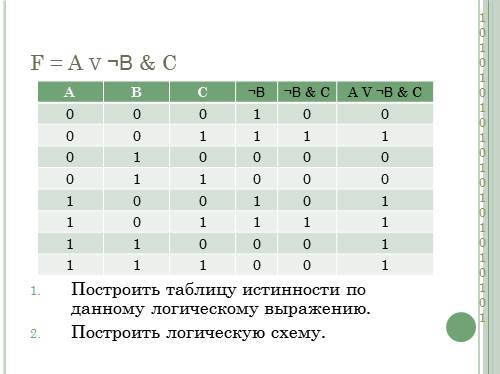
F = A v ¬В & С
Построить таблицу истинности по данному логическому выражению. |
| Слайд №13 | |
 |
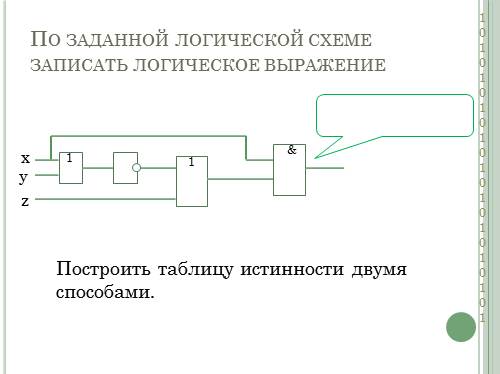
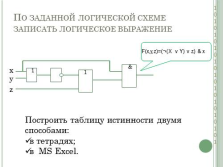
По заданной логической схеме записать логическое выражение x y z 1 1 & Построить таблицу истинности двумя способами. 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 |
| Слайд №14 | |
 |
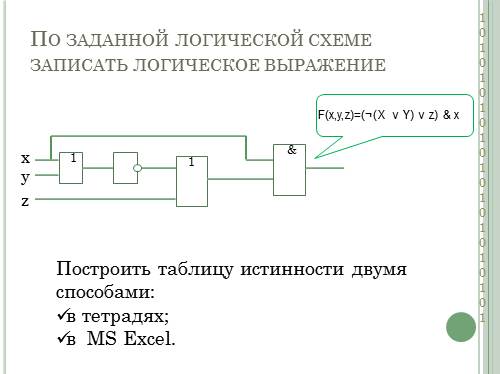
По заданной логической схеме записать логическое выражение x y z 1 1 & Построить таблицу истинности двумя способами: в тетрадях; в MS Excel. 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 F(x,y,z)=(¬(X v Y) v z) & x |
| Слайд №15 | |
 |
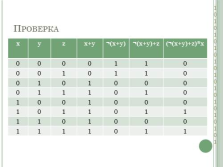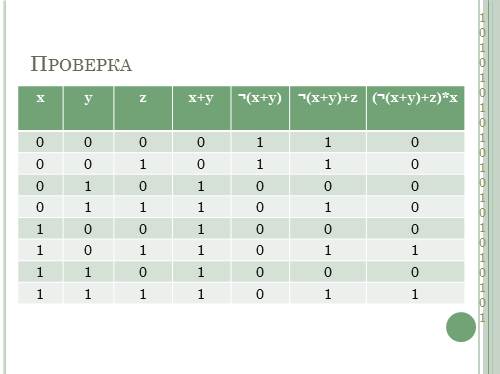
Проверка 1 0 1 0 1 0 1 0 1 0 10 1 0 10 1 0 10 1 |
| Слайд №16 | |
 |
Список литературы: Информатика и ИКТ. Профильный уровень: учебник для 10 класса . Н.Д. Угринович. М.: БИНОМ. Лаборатория знаний, 2010. Информатика. Задачник-практикум в 2 т. / Под ред. И.Г. Семакина, Е.К. Хеннера: Том 1. – М.: БИНОМ. Лаборатория знаний, 2010. |
