Подготовка к ЕГЭ. Полезно знать

Скачать презентацию (0.46 мб)

Слайды и текст этой презентации

Слайд №1
Подготовка к ЕГЭ.
Полезно знать.

Слайд №2
Задачи на смеси и сплавы
Удобно решать с использованием следующих вспомогательных средств: каждая отдельная смесь (или сплав), фигурирующая в задаче, представляется в виде таблицы, в которой записывается информация о составе данной смеси.
Слайд №3
Например, дан раствор соли с общей массой 500 и концентрацией соли 40 %. Представляем такой раствор в виде таблицы:
соль вода
40 %
60 %
500
Слева от таблицы записывается масса всего раствора. В левой колонке таблицы записывается информация об основном компоненте раствора (в данной задаче это соль).
В первой строке таблицы записывается концентрация, во второй масса компонента.
Найденная величина массы помещается во второй строке таблицы
Если при решении задачи понадобятся данные о втором компоненте раствора, то они заносятся во вторую колонку таблицы
200
300
( ).
( ; )
Слайд №4
ПРАВИЛО:
При смешивании нескольких растворов складываются как общие массы растворов, так и массы компонентов этих растворов.
Слайд №5
Задача.
Смешали 10%- ный и 25%- ный растворы соли и получили 3кг 20% -ного раствора. Какое количество каждого раствора (в кг) было использовано?
Решение
соль вода
10%
х
соль вода
25%
соль вода
20%
3
(3 – х)
=
+
0,1х
0,25(3-х)
Имеем: 0,1x + 0,25(3- x) = 0,6
0,1x + 0,75 – 0,25x = 0,6
-0,15x = -0,15
x = 1

3 – x = 3 – 1 = 2
Ответ: 1 кг; 2 кг
0,6
Слайд №6
Задача.
Сколько кг воды нужно выпарить из 0,5 т целлюлозной массы, содержащей 85% воды, чтобы получить массу с содержанием 75% воды?
Решение
цел-за вода
85%
цел-за вода
100%

—
цел-за вода
75%
0,5
х
=
0,5 · 0,85 = 0,425
0,425
(0,5-х)
0,75( 0,5 – x)
х
Имеем: 0,425 — x = 0,75( 0,5 – x)
0,425 – x = 0,375 – 0,75x

x — 0, 75x = 0,425 – 0,375

0,25x = 0,05
x = 0,2
Ответ: 200 кг
Слайд №7
Задача.
Смешали 2л 60%- ного раствора соли с 3л 50%- ного раствора соли и к смеси добавили 1л чистой воды. Какова концентрация соли в полученной смеси?
Решение
соль вода
60%
соль вода
Х %
соль вода
50%
соль вода
0%
0
2
3
1
+
+
=
=
Символы «+» между таблицами показывают, что растворы смешиваются и, следовательно, соответствующие массы складываются.
1) Находим массу соли в первом растворе:
0,6 · 2 =
1,2
2) Находим массу соли во втором растворе:
0,5 · 3 =
1,5
Для каждого раствора имеем:
Масса соли: 1,2 + 1,5 + 0 =

общая раствора: 2 + 3 + 1 =
2,7
6
Имеем: 6 — 100%

2,7 — х%
=> х = 45%
Ответ: 45%
Слайд №8
Задачи на «сухой остаток»
Задача.
В магазин привезли 100 кг клюквы, состоящей на 99% из воды. После длительного хранения и усушки содержание воды в клюкве уменьшилось до 98%. Каким стал новый вес клюквы?
Решение
клюква вода

99%
1%
100кг
1кг
1кг
клюква вода

98%
2%
1кг — 2%
Xкг — 100%
=> х = — = 50 (кг)
100
2
Ответ: 50 кг

Слайд №9
Решение
грибы вода
 
   
90%
10%
22кг
22 ? 0,1 = (кг)
2,2
– масса свежих грибов без воды
Задача.
Свежие грибы содержат по массе 90% воды, а сухие содержат 12% воды. Сколько получится сухих грибов из 22 кг свежих грибов?
грибы вода
2,2
12%
100% — 12% = сухих грибов
88%
2,2 кг — 88%
X кг — 100%

=> х = =
2,2 ? 100
88
=
22 ? 10
88
=
10
4
=
2,5 (кг)
=
Ответ: 2,5 кг
Слайд №10
Решить неравенство: (х-1) (х+8)
5-х
? 0
Решение
Нули:
1
;
-8
;
5
х
Есть промежуток, которому принадлежит число 0
На этом промежутке установим знак.
При х = 0 имеем:
( -1) ( +8)
х
х
5
— х
?
0
<
—
+
+
—
э х
(- ; -8]
8
?
[1 ; 5)
Ответ:
(- ; -8]
8
?
[1 ; 5)
Слайд №11
«Шутливые» законы
I: Увидел сумму – делай произведение
II: Увидел произведение – делай сумму
III: Увидел квадрат – понижай степень
Совет: Если не знаешь, с чего начать преобразование тригонометрических выражений (за что «зацепиться»), начни с этих законов.
Тригонометрические выражения во многих случаях подчиняются трём «законам»:
Слайд №12
Решить уравнение: sin2x ? sin6x = cosx ? cox3x
увидел произведение – делай сумму :
Решение
1
2
(cos (2x–6x) – cos (2x+6x)) =
1
2
(cos (x-3x) + cos (x+3x))
сos 4x – cos8x = cos 2x + cos4x
(- )
(- )
cos4x – cos8x = cos2x + cos4x
cos2x + cos8x = 0
увидел сумму – делай произведение :
2cos
2x+8
2
? cos
2x-8x
2
= 0
сos5x ? cos(-3x) = 0
сos5x = 0 или cos3x = 0
5x =
?
2
+
?k
или 3x
=
?
2
+
?k
x
?
10
=
?k
5
+
x
=
?
6
?k
+
3
(k Z)
Э
Слайд №13
Решить уравнение:
cos 2x + cos 3x = 1
2
2
Решение
увидел квадрат – понижай степень :
1 +
cos4x
2
+
1 +
cos6x
2
=
1
2
0
увидел сумму – делай произведение :
2cos
4x + 6x
2
?
cos
4x — 6x
2
= 0
cos5x ? cos(-x) = 0
5x =
?
2
?k
+
или
cos5x = 0 или сos(-x)=0
x
?
2
?k
+
=
?
10
?k
+
x =
5
?
10
?k
+
5
?
2
?k
+
;
Ответ:
(k Z)
Э
Слайд №14
Фронтальная работа (взаимная проверка)Предложите способ решения данного тригонометрического уравнения

1)Приведение к квадратному;
2)приведение к однородному;
3)разложение на множители;
4)понижение степени;
5)преобразование суммы тригонометрических функций в произведение
Вариант I

Уравнение Способы решения Способы решения Способы решения Способы решения Способы решения
1 2 3 4 5
3sin2x+cos2 x=1- sinxcosx
4cos2 x-cosx-1 =0
4sin2x+cos2x=1
cosx+cos3x=0
2Sinxcos5x-cos5x=0
Вариант II
Уравнение Способы решения Способы решения Способы решения Способы решения Способы решения
1 2 3 4 5
2sinxcosx – sinx=0
3cos2 x-cos2x=1
6sin2x+4 sinxcosx=1
4sin2x+11sinx=3
sin3x=sin17x

Слайд №15
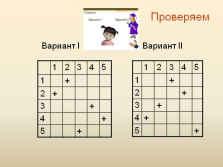Проверяем
Вариант I

Вариант II
1 2 3 4 5
1 +
2 +
3 +
4 +
5 +
1 2 3 4 5
1 +
2 +
3 +
4 +
5 +

Слайд №16
Экспертная работа
Слайд №17
Слайд №18
Слайд №19
Метод декомпозиции
Исходное неравенство
О.Д.З.
Декомпозиция неравенства (равносильное исходному на О.Д.З.)
а
f(x)
— a
g(x)
V
0
a > 0, a = 1
D(f)
D(g)
log f(x)- log g(x)V 0
a
a
а > 0, а = 1
f(x) > 0
g(x)>0
(a – 1)(f(x) – g(x))v0
(a – 1)(f(x) – g(x))v0
Слайд №20
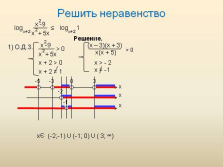Решить неравенство
1) О.Д.З.
log
x -9
x + 5x
2
2
x+2
?
log 1
x+2
Решение.
x -9
x + 5x
2
2
> 0
x + 2 > 0
x + 2 = 1
(x – 3)(x + 3)
x(x + 5)
x > — 2
x = -1
x
x
x
-5
-3
0
3
-2
-1
x
Э
(-2;-1) U (-1; 0) U ( 3; ?)
> 0
Слайд №21
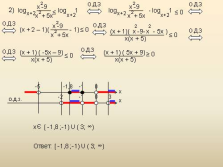2)
log
x -9
x + 5x
2
2
x+2
log 1
x+2
?
О.Д.З
(x + 2 – 1)( — 1)
x -9
x + 5x
2
2
? 0
О.Д.З
(x + 1)(
x(x + 5)
x -9
— x — 5x )
2
2
? 0
(x + 1) ( -5x – 9)
x(x + 5)
? 0
О.Д.З
(x + 1) ( 5x + 9)
x(x + 5)
? 0
x
x
-5
-1,8
-1
3
-2
0
-1
0
x
Э
[ -1,8 ;-1) U ( 3; ?)
Ответ:
[ -1,8 ;-1) U ( 3; ?)
О.Д.З
О.Д.З
О.Д.З
О.Д.З.
log —
x+2
x -9
x + 5x
2
2
log 1
x+2
? 0
О.Д.З
Слайд №22
Решить неравенство
— (0,5)

x +3x-2
2
2x +2x-1
2
x
? 0
Решение.
1) О.Д.З. 5 — 1 = 0, х = 0
x
2) На О.Д.З. имеем:
2 — 2
5 — 5

2x +6x-4
2
2
x
? 0
1-2х-2х
0
(2 – 1)(
(5 – 1)(х – 0)
2x + 6x — 4 —
2
2
(1-2х-2х ))
? 0
2x + 6x — 4 —
2
2
1+ 2х + 2х
? 0
х
4х + 8х -5
х
2
? 0
4( x — )( x +2,5)
x
? 0
0
0
x
x
x
Э
( — ? ; ] U ( 0; ]
5 — 1
-2,5
0,5
0,5
-2,5
0,5
О.Д.З
Слайд №23
Оцените статью:
  1. 5
  2. 4
  3. 3
  4. 2
  5. 1
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Похожие записи:
Массовая доля вещества в раствореМассовая доля вещества в растворе
Подготовка к ЕГЭ 2014 — Задачи В11 и В10Подготовка к ЕГЭ 2014 — Задачи В11 и В10
Первоначальные химические понятияПервоначальные химические понятия