Выражения с модулем в углублённом курсе математики 6 класса
Слайды и текст этой презентации
| Слайд №1 |
 |
Выражения с модулем в углублённом курсе математики 6 класса
Учитель математики
МБУ лицея № 51
Юганова Татьяна Васильевна |
| Слайд №2 |
 |
5/16/2014
2
Понятие «модуль» в курсе математики
Понятие абсолютной величины является одним из основных понятий элементарной математики.
Осмысленное владение понятием «модуль» помогает учащимся воспринимать алгебру и геометрию как единое целое.
“Расстояние между точками” позволяет методу координат геометрический материал изложить без единого чертежа, используя только числа и алгебраические операции.
Свойства осевой симметрии позволяют оценивать правильность найденных решений ряда уравнений, содержащих модуль, строить графики функций.
Например, в математическом анализе понятие абсолютной величины содержится в определении такого понятия, как предел.
В теории приближённых вычислений используется понятие абсолютной погрешности.
В механике, в геометрии изучаются понятия вектора, одной из характеристик которого служит его длина (модуль вектора), т. е. его абсолютная величина.
|
| Слайд №3 |
 |
5/16/2014
3
ТЕМА «МОДУЛЬ ЧИСЛА»
Федеральной программой в обязательный курс 6 класса включена тема «Модуль числа». Поурочное планирование предусматривает на изложение данной темы 2 часа.
В программе углублённого курса на эту тему отводится 3 часа, а также есть возможность использовать на неё время в дополнительном курсе «Решение олимпиадных задач».
Задачи, связанные с абсолютной величиной часто встречаются на математических олимпиадах, выпускных и вступительных экзаменах. Это понятие широко применяется не только в различных разделах школьного курса, но и в курсе высшей математики.
Поэтому важно разработать методику преподавания данной темы с самого начала таким образом, чтобы учащиеся не только усваивали основной материал, но и успешно применяли его в более сложных заданиях, развивающих их творческий потенциал.
|
| Слайд №4 |
 |
5/16/2014
4
«МОДУЛЬ» в учебниках
Понятие модуля является непростым для восприятия большинством учеников на начальном этапе.
В учебниках математики первоначальное понятие модуля вводится по-разному:
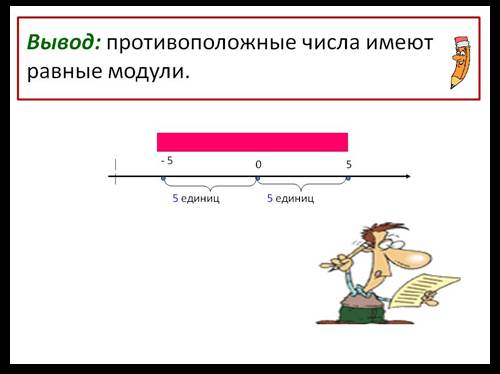
как расстояние от точки изображающей число до начала координат (Математика. Н.Я. Виленкин)
как длина вектора (Математика. П.М. Эрдниев)
как число “без знака” (Математика. Г.В. Дорофеев)
Рассмотрим один из вариантов введения данного понятия на базовом уровне по учебнику
Н.Я. Виленкина и др.
ТЕМА «МОДУЛЬ ЧИСЛА» |
| Слайд №5 |
 |
5/16/2014
5 |
| Слайд №6 |
 |
5/16/2014
6 |
| Слайд №7 |
 |
5/16/2014
7 |
| Слайд №8 |
 |
5/16/2014
8 |
| Слайд №9 |
 |
5/16/2014
9 |
| Слайд №10 |
 |
5/16/2014
10 |
| Слайд №11 |
 |
5/16/2014
11 |
| Слайд №12 |
 |
5/16/2014
12
|
| Слайд №13 |
 |
5/16/2014
13 |
| Слайд №14 |
 |
5/16/2014
14 |
| Слайд №15 |
 |
5/16/2014
15 |
| Слайд №16 |
 |
5/16/2014
16 |
| Слайд №17 |
 |
5/16/2014
17 |
| Слайд №18 |
 |
5/16/2014
18 |
| Слайд №19 |
 |
5/16/2014
19 |
| Слайд №20 |
 |
5/16/2014
20 |
| Слайд №21 |
 |
5/16/2014
21 |
| Слайд №22 |
 |
5/16/2014
22
Дидактические материалы
Пособие авторов Чесноков А.С. И Нешков К.И. содержит самостоятельные и контрольные работы идентичные по степени трудности вариантов, в которых первые четыре задания служат для проверки усвоения пройденного материала, а пятое требует проявления смекалки.
Пособие авторов А.П. Ершова, В.В. Голобородько содержит самостоятельные и контрольные работы из
6 вариантов трёх уровней сложности для организации дифференцированной работы учащихся ( уровень А – обязательный, Б – средний уровень сложности, В – для учеников, проявляющих повышенный интерес к математике, а также для использования в школах, гимназиях и лицеях с углубленным изучением математики) |
| Слайд №23 |
 |
5/16/2014
23
Самостоятельные и контрольные работы А.П. Ершова, В.В. Голобородько
|
| Слайд №24 |
 |
5/16/2014
24
С – 21 А |
| Слайд №25 |
 |
5/16/2014
25
С – 21 А |
| Слайд №26 |
 |
5/16/2014
26
С – 21 Б |
| Слайд №27 |
 |
5/16/2014
27
С – 21 Б |
| Слайд №28 |
 |
5/16/2014
28
С – 21 |
| Слайд №29 |
 |
5/16/2014
29 |
| Слайд №30 |
 |
5/16/2014
30 |
| Слайд №31 |
 |
5/16/2014
31 |
| Слайд №32 |
 |
5/16/2014
32
К – 8 В |
| Слайд №33 |
 |
5/16/2014
33 |
| Слайд №34 |
 |
5/16/2014
34 |
| Слайд №35 |
 |
5/16/2014
35
С – 28* |
| Слайд №36 |
 |
5/16/2014
36
К – 10, К — 11 |
| Слайд №37 |
 |
5/16/2014
37
К – 14 итоговая |
| Слайд №38 |
 |
5/16/2014
38
Всё гениальное – просто, а всё простое – гениально?
Простота — это то, что труднее всего на свете; это крайний предел опытности и последнее усилие гения. Жорж Санд
Все должно быть изложено так просто, как только возможно… Альберт Эйнштейн
Сделать простое сложным может каждый. Сделать сложное простым , простым до изумления – это и есть творчество . Чарльз Мингус .
|
| Слайд №39 |
 |
5/16/2014
39
Как выглядит простота?
Истинной простоты не может быть бесконечно много.
Если искать её среди чисел, то простота – это число три.
Это «самое» простое число как с физической, так и с математической точки зрения.
Три – это устойчивость (минимальное количество ножек у стола – три).
Пространственные фигуры трёхмерны.
И любой список из множества пунктов можно свести к трем основным. В этой работе тоже «три по три» принципа простоты: 1. три части в изложении материала (вводная, основная, заключительная)
2. три дидактические единицы в раскрытии темы (понятие, свойства, задачи)
3. три уровня дифференциации сложности заданий (основной, средний, углубленный)
|
| Слайд №40 |
 |
Умный каждый день пополняет свои знания. Мудрый каждый день стирает лишнее.
Лао Цзы |
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Большой сборник презентаций в помощь школьнику.
закрыть
Скопируйте этот код и вставьте его на своем сайте: