Квадратные уравнения

Главная Алгебра

Скачать презентацию (2.91 мб)

Слайды и текст этой презентации

Слайд №1
	Квадратные уравнения

Слайд №2
	Квадратное уравнение имеетдействительные положительные корни, если
Слайд №3
	Квадратное уравнение имеетдействительные отрицательные корни, если
Слайд №4
	Квадратное уравнение имеет действительные корни различных знаков, причем положительный корень имеет больший модуль, если
Слайд №5
	Квадратное уравнение имеет действительные корни различных знаков, причем отрицательный корень имеет больший модуль, если
Слайд №6
	Расположение корней относительно заданной точки определяется направлением ветвей соответствующей параболы, координатами вершины и значениями в заданных точках. В этих задачах хорошо работают графические иллюстрации.
Слайд №7
	М М
Слайд №8
	М М
Слайд №9
	М М
Слайд №10
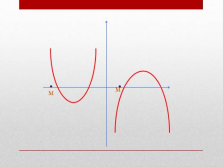
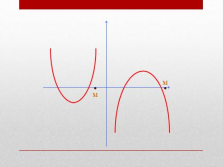
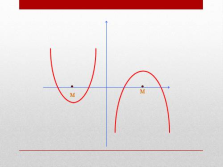
	Оба корня квадратного трехчлена меньше числа М, тогда и только тогда, когда или
Слайд №11
	Оба корня квадратного трехчлена больше числа М, тогда и только тогда, когда или
Слайд №12
	Один из корней квадратного трехчленаменьше числа М, а другой больше числа М, тогда и только тогда, когда или
Слайд №13
	При каких значениях параметра m уравнение имеет не более одного действительного корня?
Слайд №14
	При каких значениях параметра m корни уравнения различны и положительны?
Слайд №15
	При каких значениях параметра а корни уравнения таковы, что сумма их квадратов равна 1,75?
Слайд №16
	Нахождение значений параметра, при которых решения удовлетворяют некоторому условию.
Слайд №17
	Решение уравнений для всех значений параметра а
Слайд №18
	М М
Слайд №19
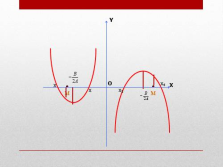	М М
Слайд №20
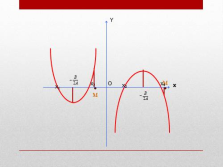	М М
Слайд №21
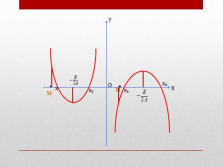
	Оба корня квадратного уравнения больше заданного числа М тогда и только тогда, когда имеет место система Оба корня квадратного уравнения меньше заданного числа М тогда и только тогда, когда имеет место система Заданное число М лежит между корнями тогда и только тогда, когда имеет место неравенство Af(M)<0
Слайд №22
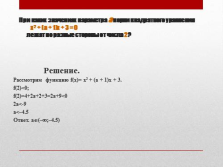	При каких значениях параметра а корни квадратного уравнения х2 + (а + 1)х + 3 = 0 лежат по разные стороны от числа 2? Решение. Рассмотрим функцию f(x)= х2 + (а + 1)х + 3. f(2)<0; f(2)=4+2a+2+3=2a+9<0 2a<-9 a<–4.5 Ответ. a?(–?;–4.5)
Слайд №23
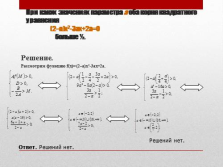	При каких значениях параметра а оба корня квадратного уравнения (2–a)x2-3ax+2a=0 больше ?. Решение. Рассмотрим функцию f(x)= (2–a)x2-3ax+2a. Решений нет. Ответ. Решений нет.
Слайд №24
	Найти все значения параметра а, при которых оба корня квадратного уравнения x2- 6ax+(2-2a+9a2)=0 больше 3. Решение. Рассмотрим функцию f(x)= x2-6ax+(2-2a+9a2) a? Ответ:
Слайд №25
	Найти все значения параметра а, которых оба корня квадратного уравнения x2+4ax+(1-2a+4a2)=0 меньше –1. Решение. Рассмотрим функцию f(x)= x2+4ax+(1-2a+4a2). Ответ. a? .