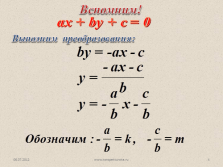Линейная функция и ее график
Скачать презентацию (0.16 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Линейная функция 7 классалгебра Урок № 8 Линейная функция и ее график 06.07.2012 1 www.konspekturoka.ru |
| Слайд №2 | |
 |
Цели: 06.07.2012 Повторить алгоритм построения графика линейного уравнения с двумя переменными. Рассмотреть линейную функцию и ее график. Научить строить и читать график y = kx + b. 2 www.konspekturoka.ru |
| Слайд №3 | |
 |
06.07.2012 www.konspekturoka.ru 3 Алгоритм построения графика уравнения ах + bу + c = 0 3. Построим на координатной плоскости точки (х?; у?), (х?; у?) и соединим прямой. 4. Прямая – есть график уравнения. Вспомним! Внимание! Этот способ не удобен! |
| Слайд №4 | |
 |
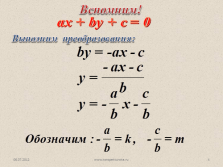ах + by + c = 0 06.07.2012 4 www.konspekturoka.ru Вспомним! Выполним преобразования: |
| Слайд №5 | |
 |
06.07.2012 www.konspekturoka.ru 5 y = kx + m Частный вид линейного уравнения с двумя переменными называется линейной функцией. y – независимая переменная х – зависимая переменная Графиком линейной функции y = kx + m есть прямая. Теорема: |
| Слайд №6 | |
 |
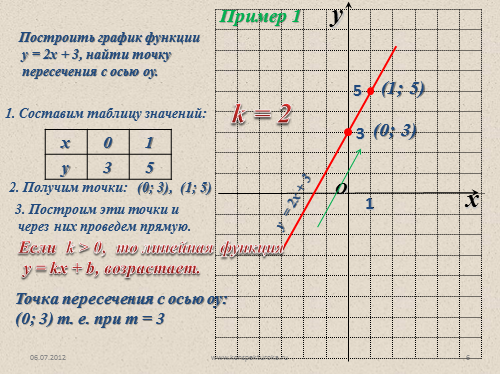
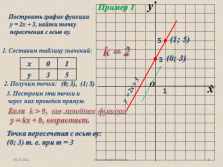
06.07.2012 www.konspekturoka.ru 6 Пример 1 Построить график функции у = 2х + 3, найти точку пересечения с осью оу. 1. Составим таблицу значений: 2. Получим точки: (0; 3), (1; 5) 3. Построим эти точки и через них проведем прямую. (0; 3) 3 (1; 5) у = 2х + 3 Если k > 0, то линейная функция у = kx + b, возрастает. k = 2 Точка пересечения с осью оу: (0; 3) т. е. при т = 3 |
| Слайд №7 | |
 |
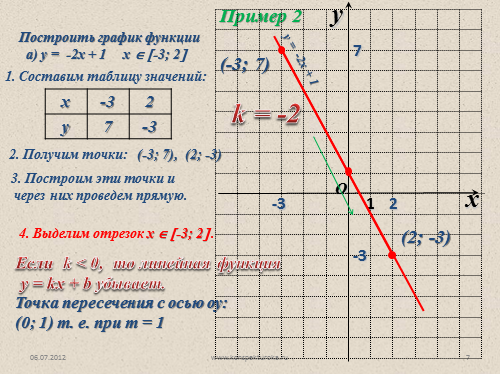
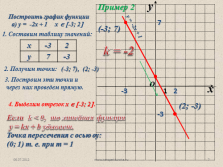
06.07.2012 www.konspekturoka.ru 7 Пример 2 Построить график функции а) у = -2х + 1 х ? ?-3; 2? 1. Составим таблицу значений: 2. Получим точки: (-3; 7), (2; -3) 3. Построим эти точки и через них проведем прямую. (-3; 7) (2; -3) 4. Выделим отрезок х ? ?-3; 2? . Если k < 0, то линейная функция у = kx + b убывает. k = -2 у = -2х + 1 Точка пересечения с осью оу: (0; 1) т. е. при т = 1 |
| Слайд №8 | |
 |
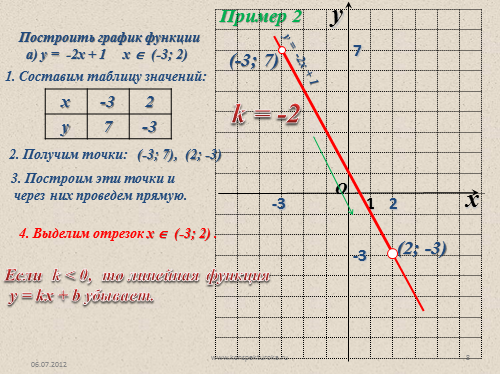
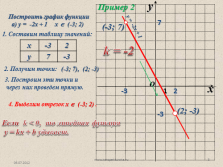
06.07.2012 www.konspekturoka.ru 8 Пример 2 Построить график функции а) у = -2х + 1 х ? (-3; 2) 1. Составим таблицу значений: 2. Получим точки: (-3; 7), (2; -3) 3. Построим эти точки и через них проведем прямую. (-3; 7) (2; -3) 4. Выделим отрезок х ? (-3; 2) . Если k < 0, то линейная функция у = kx + b убывает. k = -2 у = -2х + 1 |
| Слайд №9 | |
 |
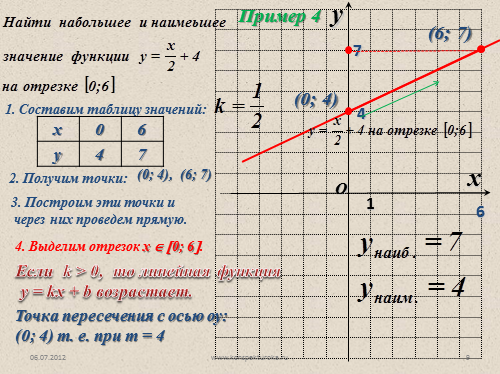
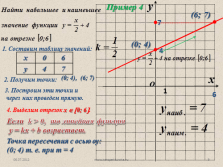
06.07.2012 www.konspekturoka.ru 9 Пример 4 1. Составим таблицу значений: 2. Получим точки: (0; 4), (6; 7) 3. Построим эти точки и через них проведем прямую. 4 (0; 4) 4. Выделим отрезок х ? ?0; 6?. (6; 7) Если k > 0, то линейная функция у = kx + b возрастает. Точка пересечения с осью оу: (0; 4) т. е. при т = 4 |
| Слайд №10 | |
 |
06.07.2012 www.konspekturoka.ru 10 Вывод: Функция y = kx + m называется возрастающей, если большему значению аргумента соответствует большее значение функции (двигаясь по графику функции, мы поднимаемся вверх). Функция y = kx + m называется убывающей, если большему значению аргумента соответствует меньшее значение функции (двигаясь по графику функции, мы опускаемся вниз). |
| Слайд №11 | |
 |
06.07.2012 www.konspekturoka.ru 11 Вывод: Величина k определяет наклон графика функции y = kx + m Если k < 0, то линейная функция у = kx + b убывает. Если k > 0, то линейная функция у = kx + b возрастает. Если k = 0, то линейная функция у = kx + b параллельна оси абсцисс (или совпадает с ней). |
| Слайд №12 | |
 |
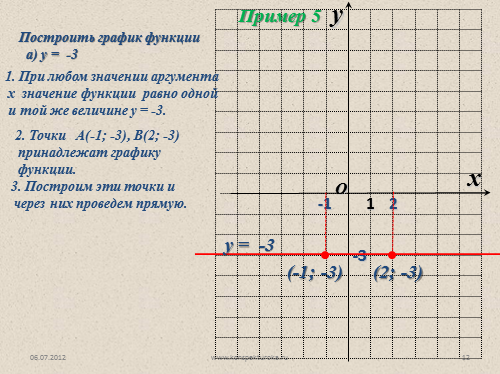
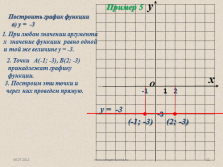
06.07.2012 www.konspekturoka.ru 12 Построить график функции а) у = -3 1. При любом значении аргумента х значение функции равно одной и той же величине у = -3. 2. Точки А(-1; -3), В(2; -3) принадлежат графику функции. 3. Построим эти точки и через них проведем прямую. (-1; -3) (2; -3) у = -3 Пример 5 |
| Слайд №13 | |
 |
06.07.2012 13 www.konspekturoka.ru Ответить на вопросы: 1. Какой алгоритм построения графика линейного уравнения с двумя переменными? 2. Какую функцию называют линейной функцией? 3. Что является графиком линейной функции? Как можно построить такой график? 4. Как найти точку пересечения графика с осью оу? 5. Смысл величин k и m в формуле линейной функции? 6. Какая прямая будет графиком функции при k = 0? 7. Дайте определение возрастающей (убывающей) функций. 8. Как влияет k на возрастание (убывание) функции? |
