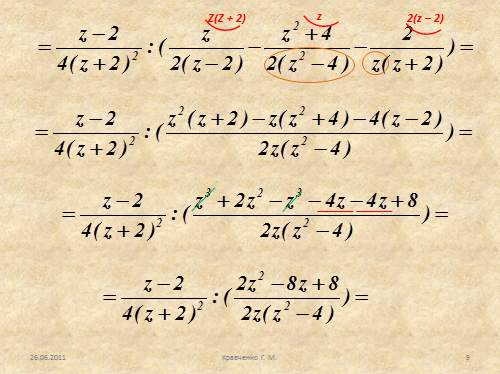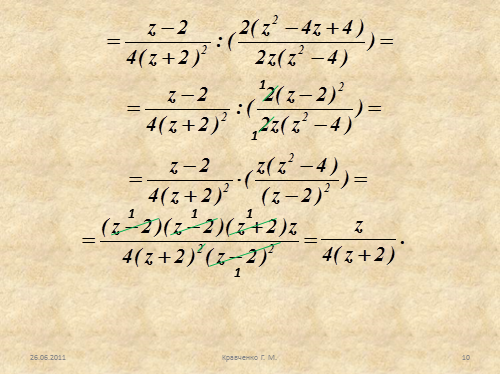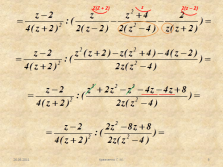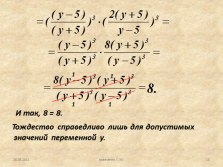Преобразование рациональных выражений
Скачать презентацию (0.19 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Алгебраические дроби 6. Преобразование рациональных выражений (уроки 17 — 18). 26.06.2011 8 классалгебра 1 Кравченко Г. М. |
| Слайд №2 | |
 |
Изучить правила преобразования рациональных выражений; Научиться упрощать выражения; Научиться доказывать тождества. Цели: 26.06.2011 2 Кравченко Г. М. |
| Слайд №3 | |
 |
26.06.2011 Кравченко Г. М. 3 Рациональные числа — все целые числа и все дроби, как положительные так и отрицательные. Целое выражение — выражение представленное в виде многочлена . Дробное выражение – это алгебраическая дробь. Рациональное выражение – алгебраическое выражение составленное из чисел и переменных с помощью арифметических операций и возведения в натуральную степень. |
| Слайд №4 | |
 |
26.06.2011 Кравченко Г. М. 4 Для преобразования рациональных выражений принят тот же порядок действий, что и для преобразования числовых выражений. Это значит, что сначала выполняют действия в скобках, затем действия второй ступени (умножение, деление, возведение в степень), а затем действия первой ступени (сложение, вычитание). Рассмотрим наиболее сложные задания: Изучение новой темы |
| Слайд №5 | |
 |
26.06.2011 Кравченко Г. М. 5 Рассмотрим пример 1. Упростить выражение. 1 1 1 1 |
| Слайд №6 | |
 |
26.06.2011 Кравченко Г. М. 6 Решение Рассмотрим пример 2. Упростить выражение: Для упрощения выражения выбираем способ преобразования по действиям. |
| Слайд №7 | |
 |
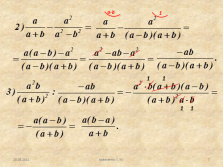26.06.2011 Кравченко Г. М. 7 1 1 1 1 |
| Слайд №8 | |
 |
26.06.2011 Кравченко Г. М. 8 Рассмотрим пример 3. Упростить выражение: |
| Слайд №9 | |
 |
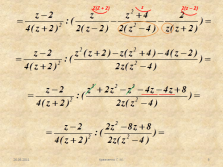26.06.2011 9 Кравченко Г. М. |
| Слайд №10 | |
 |
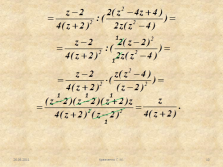26.06.2011 Кравченко Г. М. 10 1 1 1 1 1 1 |
| Слайд №11 | |
 |
26.06.2011 Кравченко Г. М. 11 Доказать тождество – это значит установить, что при всех допустимых значениях переменной его левая и правая части тождественно равные выражения. Способы доказательства тождеств: Преобразовывают левую часть и получают в итоге правую часть; 2)Преобразовывают правую часть и получают в итоге левую часть; 3)По отдельности преобразовывают правую, а затем левую часть и в итоге получают равные выражения; 4) Составляют разность левой и правой части и в итоге получают нуль. Какой способ выбрать – зависит от конкретного вида тождества, которое предлагают доказать. |
| Слайд №12 | |
 |
26.06.2011 Кравченко Г. М. 12 Рассмотрим пример 4. Доказать тождество. Для доказательства тождества выбираем первый способ: преобразуем левую часть. Решение 1 |
| Слайд №13 | |
 |
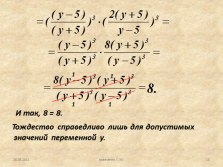26.06.2011 Кравченко Г. М. 13 1 1 1 1 И так, 8 = 8. Тождество справедливо лишь для допустимых значений переменной у. |
| Слайд №14 | |
 |
Ответить на вопросы: 26.06.2011 14 Кравченко Г. М. Какие числа называются рациональными? Какое выражение называется дробным? Какое выражение называется рациональным? Что значит доказать тождество? Какие способы доказательства тождества можно назвать? |
