Разбор некоторых решений задания С2 ЕГЭ по математике

Главная Алгебра

Скачать презентацию (0.22 мб)

Слайды и текст этой презентации

Слайд №1

Девиз урока: « Дорогу осилит идущий, а математику – мыслящий.»
« Три качества:
обширные знания, привычка мыслить и благородство чувств –
необходимы для того, чтобы человек был образованным
в полном смысле слова»
Н.Г.Чернышевский

Слайд №2
	Цели урока: Закрепление знаний, умений и навыков по изученной теме, устранение пробелов. 2. Совершенствование навыков решения задач на применение теоремы о трех перпендикулярах, теоремы о площади ортогональной проекции произвольного многоугольника, понятия двугранного угла. Применение этих теорем в решении задач С2 ЕГЭ. Развитие логического мышления и речи: умение логически обосновывать суждения, проводить систематизации.
Слайд №3
	Тест с последующей самопроверкой Двугранный угол, образованный полуплоскостями измеряется величиной его………………., получаемого при пересечении двугранного угла плоскостью, ………………….его ребру. 2. Двугранный угол имеет ……………..множество линейных углов. 3. Площадь ортогональной проекции многоугольника на плоскость равна ………………..его площади на…………. угла между плоскостью многоугольника и плоскостью проекции. 4. Прямая, проведенная в плоскости через основание наклонной ……………..к её проекции на эту плоскость, ………………..и к самой……………… 5. Высотой призмы называется ………………между плоскостями её оснований. 6. Призма называется прямой, если её боковые ребра……………… основаниям. 7……………призма называется правильной, если её основания являются …………….многоугольниками. 8. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть …………………….между ……………катетов на гипотенузу. 9. Катет прямоугольного треугольника есть ………………..между гипотенузой и …………..этого катета на гипотенузу.
Слайд №4
	Ответы к тесту : Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру. Двугранный угол имеет бесконечное множество линейных углов. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции. 4. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость перпендикулярна и к самой наклонной. 5. Высотой призмы называется расстояние между плоскостями её оснований. 6.Призма называется прямой, если её боковые ребра перпендикулярны основаниям. 7. Прямая призма называется правильной, если её основания являются правильными многоугольниками. 8.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу. 9. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
Слайд №5
	Задача ( С2 ЕГЭ 2010 г.) В прямоугольном параллелепипеде ABCDA1B1C1D1 , у которого AB = 6, BC = 6, CC1 = 4, найдите тангенс угла между плоскостями ACD1 и A1B1C1. A1 B1 C1 D1 Решение 1. Вместо плоскости A1B1C1 возьмем параллельную ей плоскость ABC. 2. Пусть – E середина АC. DE ? AC, D1E ? AC по теореме о ТТП. 4. Из прямоугольного треугольника D1DE находим: Ответ: А B C D E
Слайд №6
	Задача. В правильной треугольной призме, каждое ребро которой равно 9 дм, постройте сечение, проходящее через сторону основания и середину отрезка, соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сечения призмы.
Слайд №7
	Задача. В правильной треугольной призме, каждое ребро которой равно 9 дм, постройте сечение, проходящее через сторону основания и середину отрезка, соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сечения призмы.
Слайд №8
	Задача. В правильной треугольной призме, каждое ребро которой равно 9 дм, постройте сечение, проходящее через сторону основания и середину отрезка, соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сечения призмы.
Слайд №9
	Задача. В правильной треугольной призме, каждое ребро которой равно 9 дм, постройте сечение, проходящее через сторону основания и середину отрезка, соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сечения призмы.
Слайд №10
	Задача. В правильной треугольной призме, каждое ребро которой равно 9 дм, постройте сечение, проходящее через сторону основания и середину отрезка, соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сечения призмы.
Слайд №11
	Задача. В правильной треугольной призме, каждое ребро которой равно 9 дм, постройте сечение, проходящее через сторону основания и середину отрезка, соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сечения призмы.
Слайд №12
	Задача. В правильной треугольной призме, каждое ребро которой равно 9 дм, постройте сечение, проходящее через сторону основания и середину отрезка, соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сечения призмы.
Слайд №13
	Задача. В правильной треугольной призме, каждое ребро которой равно 9 дм, постройте сечение, проходящее через сторону основания и середину отрезка, соединяющего центры оснований призмы. Найдите: а) угол между плоскостью сечения и плоскостью основания призмы; б) площадь сечения призмы.
Слайд №14
	Решение Пусть ОО1 – отрезок, соединяющий центры АВС и А1В1С1 оснований данной призмы АВСА1В1С1, К и К1 – середины ВС и В1С1. 2. ( ВСЕ) ? ( А1В1С1) = МН, МН II В1C1 , В1C1 = 3 МН, откуда следует, что S?A1MH = S?A1В1С1, значит SВ1MHС1 = S?A1В1С1 = 4. А1К1 ? В1С1 , В1С1II МН, то А1К1 ? МН, значит, KL ? MH ( где L = MH ? А1К1). Тогда по теореме о трех перпендикулярах KL ? ВС, поэтому АКL = ? – линейный угол двугранного угла между секущей плоскостью и плоскостью основания призмы. Это означает, что S = SВ1МНС1 cos ? .
Слайд №15
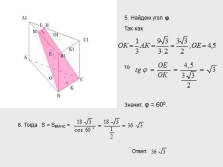	5. Найдем угол ?. то Значит, ? = 600. 6. Тогда S = SВМНС = Ответ: Так как
Слайд №16
	Домашнее задание ЕГЭ В4: В треугольнике ABC угол C равен 900, Найдите высоту CH. 2) В прямоугольном параллелепипеде ABCDA1 B1C1 D1 , у которого AB = 4, BC = 6, CC1 = 4, найдите тангенс угла между плоскостями CDD1 и BDA1. 3) С4 ЕГЭ 2010г.) Прямая, проведённая через середину N стороны AB квадрата ABCD , пересекает прямые CD и AD в точках M и T соответственно, и образует с прямой AB угол, тангенс которого равен 4. Найдите площадь треугольника BMT, если сторона квадрата ABCD равна 8.
Слайд №17