Степень и её свойства
Скачать презентацию (7.84 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Степень и её свойства Смирнова Светлана Вячеславовна МОУ СОШ № 39, г. Владимир |
| Слайд №2 | |
 |
Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь. М.В. Ломоносов |
| Слайд №3 | |
 |
ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!! Определение степени = раз n а п а а а • • • |
| Слайд №4 | |
 |
1. Запишите произведение в виде степени: Примеры применения 9·9·9 = 9? (-х)(-х)(-х)(-х)(-х) = (а-с)(а-с) = 2. Найдите значение степени: (-2)? = = (- 0,1)? = (- х)? (а – с)? 16 — 0,001 — 1 32 — |
| Слайд №5 | |
 |
10? — 3? = (10 -3)? = (6 — 8)? = 10 — 5·2? = — 1? + ( -2)? = — 6? — ( -1)? = 7? = ( -2)? = 10 — 5·16 = 10 — 80 = — 1 — 8 = — 36 — 1 = 100 – 9 = 91 49 — 32 — 70 — 9 — 37 |
| Слайд №6 | |
 |
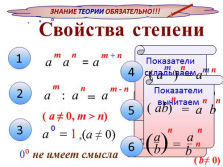ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!! Показатели умножаем Показатели складываем a a a т т — п : = ( а ? 0, т > п) Показатели вычитаем а 1 ,(а ? 0) n а b n n ( а ) = а т п т п 1 a a a = т + п т п 2 п 3 = 0 4 ( аb) = 5 0? не имеет смысла 6 а b — b — а n n n ( ( = b ? 0 ( ) |
| Слайд №7 | |
 |
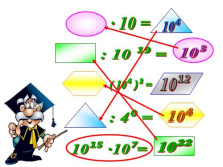10?? 10?? 10? 10? 10? 10? 10? 10? 10?? |
| Слайд №8 | |
 |
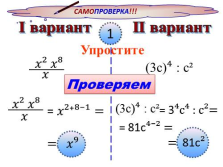САМОПРОВЕРКА!!! I вариант II вариант 1 Упростите ????? ????? ???? (3с)? : с? Проверяем ????? ????? ???? = ????????? = = ????? |
| Слайд №9 | |
 |
САМОПРОВЕРКА!!! I вариант II вариант 2 Вычислите Проверяем 25?? : 5?? |
| Слайд №10 | |
 |
САМОПРОВЕРКА!!! I вариант II вариант 3 Найдите значение выражения 2? · (2?)? 2?? Проверяем (5?)? · 5? |
| Слайд №11 | |
 |
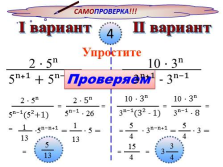САМОПРОВЕРКА!!! I вариант II вариант 4 Упростите 2 · 5? 5??? + 5??? Проверяем 10 · 3? |
| Слайд №12 | |
 |
САМОПРОВЕРКА!!! I вариант II вариант 5 Вычислите ( — 2? )? ( ( 1? )? )? 6 Сравните с нулем (-5)? · (-3,2)?… 0 -3,92? · (- 4)?… 0 |
| Слайд №13 | |
 |
Верно ли выполнены действия? 5·5·5·5 = 4? ( — 2х )? = — 2х? (- 3)? = — 9 2? · 2? = 2?? 3?? : 3? = 3? 2? + 2? = 2? 5? · 5? = 25? 5? 12 2?? 9 — 8х? 5? |
| Слайд №14 | |
 |
История создания современной теории степеней Выполните вычисления. Заполните таблицы буквами, учитывая найденные ответы. 0,4? 0,2? (- 0,6)? (- 0,1)? 1,1? (- 1,2)? (- 1,5)? — 1,4? с р т к д е и а в о м н |
| Слайд №15 | |
 |
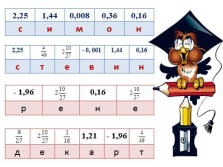2,25 1,44 0,008 0,36 0,16 с и м о н 2,25 — 0, 001 1,44 0,16 с т е в и н — 1,96 0,16 р е н е 1,21 — 1,96 д е к а р т |
| Слайд №16 | |
 |
Си?мон Сте?вин (нидерл. Simon Stevin, 1548—1620) — фламандский математик-универсал, инженер. Нидерландский математик Симон Стевин в 16-17 веках предпринял первые шаги к построению современной теории степени. Он обозначал неизвестную величину кружком, а внутри его указывал показатели степени. Запись 3(3)+5(2)–4 обозначала такую современную запись 33 + 52 – 4 |
| Слайд №17 | |
 |
Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2. Позднее Ньютон распространил эту форму записи на отрицательные и дробные показатели (1676), трактовку которых к этому времени уже предложил Стевин. Мыслю, следовательно существую. Рене Декарт Французский философ и математик. |
| Слайд №18 | |
 |
Величие человека – в его способности мыслить. Б.Паскаль а?? а * : а?? = а? а а* = а? ( а? )? ? = а?? ( a? b )* = a?? b? ( ? a* b? )? = 8 a? b?? 3 6 a?? 5 2 3 |
| Слайд №19 | |
 |
1 Дорогу осилит идущий, а математику мыслящий. Т. Эдисон Вычислите: 5??+ 5?? + 5?? + 5?? + 5?? 5?? |
| Слайд №20 | |
 |
Запишите число 9 четырьмя тройками с использованием знаков действий (включая возведение в степень). 2 9 = 3? = 3? ? ? = 3 ?? 3 3 3 Запишите число 1024 четырьмя четвёрками с использованием знаков действий (включая возведение в степень). 1024 = 2?? = 4? = 4??? = 4?? 4 ? |
| Слайд №21 | |
 |
Домашнее задание п.п. 18 – 20, № 535(б,г,е), 547. Заполните свободные клетки квадрата так, чтобы произведение выражений каждого столбца, каждой строки и диагонали равнялось Такой квадрат называется магическим. |
| Слайд №22 | |
 |
Высшее назначение математики – находить порядок в хаосе, который нас окружает. Норберт Винер |
| Слайд №23 | |
 |
Тест № 11 Свойства степени с натуральным показателем Вариант 1 Вариант 2 стр. 38 стр. 40 |
| Слайд №24 | |
 |
Математика выявляет порядок, симметрию и определённость, а это – важнейшие виды прекрасного. Аристотель Мир фракталов |
| Слайд №25 | |
 |
|
