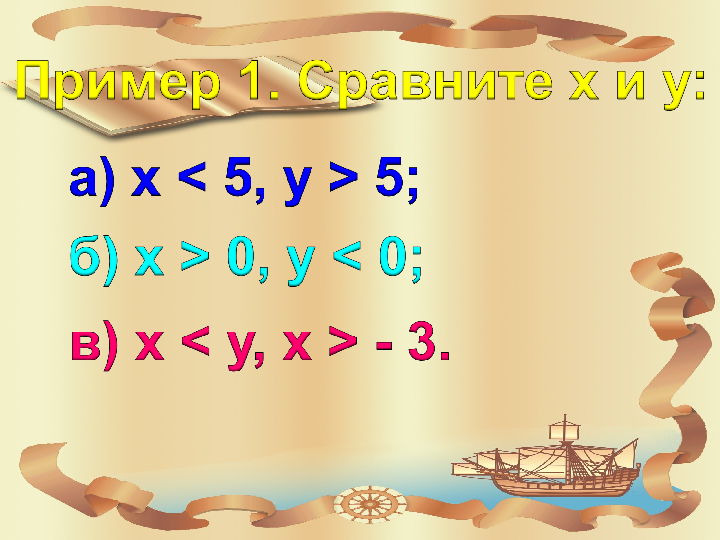Презентация на тему «Свойства числовых неравенств» (8 класс)
Слайды и текст этой презентации
Свойство 3:
Если a > b, и т < 0, то a∙т < b∙т.
Если обе части неравенства умножить
на одно и то же положительное число,
то знак неравенства сохранится;
Если обе части неравенства умножить
на одно и то же отрицательное число,
то знак неравенства изменится на противоположный
Если изменить знаки у обеих частей неравенства,
то надо изменить и знак неравенства:
если а > b, то — а < — b.
Если a > b, и т > 0, то a∙т > b∙т.
Свойство 4:
Доказательство:
I способ.
а > b и c > d – (a – b) и (c – d) – положитель-
ные числа соответственно.
(a — b) + (c — d) – положительное число.
(a — b) + (c — d) = а – b + с – d = (а + с) – (b + d) –
положительное число
Следовательно, а + с > b + d
II способ.
а > b → a + с > b + c
c > d → с + b > d + b
а + с > b + d
Если сложить почленно два неравенства одного знака, то получим неравенство того же знака.
Если a > b и c > d, то a + с > b + d.
Свойство 5:
Доказательство:
а > b и c > 0 → a ∙ с > b ∙ c
а ∙ с > b ∙ d
с > d и b > 0 → с ∙ b > d ∙ b
При умножении неравенств одинакового знака,
у которых левые и правые части —
положительные числа,
получится неравенство того же знака.
Если a, b, c, d – положительные числа и а > b, c > d, то a ∙ с > b ∙ d
Свойство 6:
Если обе части неравенства — неотрицательные числа, то их можно возвести в одну и ту же натуральную степень, сохранив знак неравенства.
Если п — нечетное число, то для любых чисел а и b из неравенства а > b следует неравенство того же знака an >bn