Компланарные векторы
Скачать презентацию (0.23 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Компланарные векторы Урок 5 |
| Слайд №2 | |
 |
Цели урока Ввести определение компланарных векторов. Рассмотреть признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов. |
| Слайд №3 | |
 |
Новый материал Определение. Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости. Иначе: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости. Любые два вектора компланарны. Три вектора, среди которых имеются два коллинеарных, также компланарны. Почему? Три произвольных вектора могут быть как компланарными, так и некомпланарными. |
| Слайд №4 | |
 |
Новый материал Устно: 355 |
| Слайд №5 | |
 |
Новый материал Признак компланарности трех векторов: |
| Слайд №6 | |
 |
Новый материал Признак компланарности трех векторов: • О А1 В1 С |
| Слайд №7 | |
 |
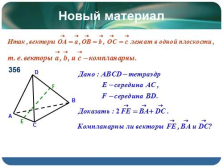Новый материал 356 |
| Слайд №8 | |
 |
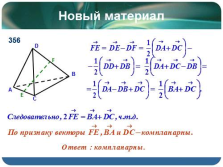Новый материал 356 |
| Слайд №9 | |
 |
Новый материал Определение. Утверждение, обратное признаку компланарности векторов: Докажем это. |
| Слайд №10 | |
 |
Новый материал О А В Р Р1 Так как векторы компланарны, то они лежат в одной плоскости. |
| Слайд №11 | |
 |
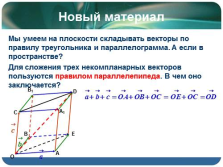Новый материал Мы умеем на плоскости складывать векторы по правилу треугольника и параллелограмма. А если в пространстве? Для сложения трех некомпланарных векторов пользуются правилом параллелепипеда. В чем оно заключается? Е С В А О D B1 A1 |
| Слайд №12 | |
 |
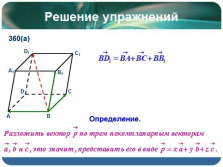Решение упражнений 360(а) Определение. |
| Слайд №13 | |
 |
Домашнее задание п. 39, 40 вопросы 13-15 стр. 97 358, 360(б), 368(а, б) |
| Слайд №14 | |
 |
|
