Решение задач на применение аксиом стереометрии и их следствий

Главная Геометрия

Скачать презентацию (0.19 мб)

Слайды и текст этой презентации

Слайд №1
	Аксиомы стереометрии 10 классгеометрия 3. Решение задач на применение аксиом стереометрии и их следствий 1 10.03.2014 www.konspekturoka.ru

Слайд №2
	Цели: Повторить аксиомы стереометрии: — о взаимном расположении точек, — о взаимном расположении прямых, — о взаимном расположении плоскостей в пространстве. Повторить следствия из аксиом стереометрии. Формировать навык применения аксиом стереометрии и их следствий при решении задач. 2 10.03.2014 www.konspekturoka.ru
Слайд №3
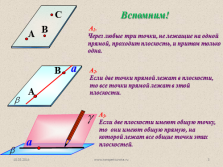	А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 10.03.2014 3 www.konspekturoka.ru Вспомним!
Слайд №4
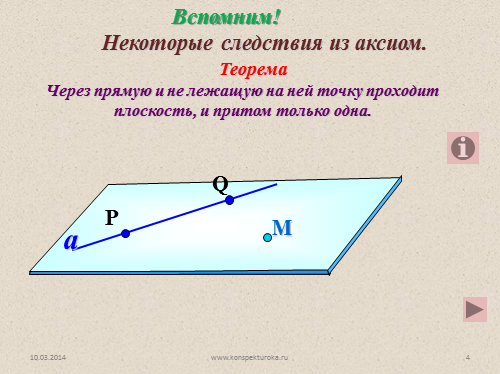
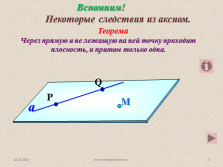
	Некоторые следствия из аксиом. Теорема Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. М a 10.03.2014 4 www.konspekturoka.ru Вспомним!
Слайд №5
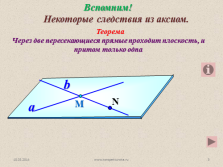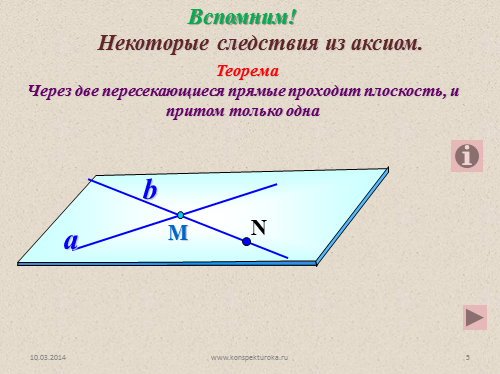
	Теорема Через две пересекающиеся прямые проходит плоскость, и притом только одна М a b N 10.03.2014 5 www.konspekturoka.ru Некоторые следствия из аксиом. Вспомним!
Слайд №6
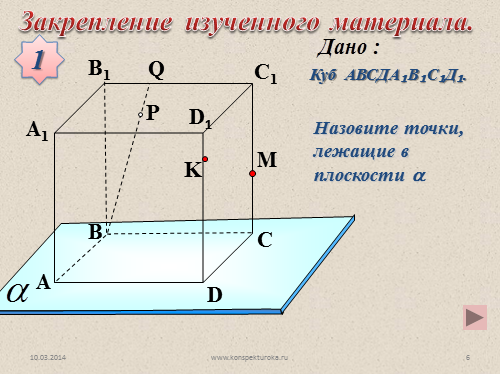
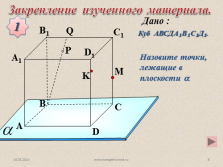
	P A B C D A1 B1 C1 D1 M K Q Назовите точки, лежащие в плоскости ? 10.03.2014 6 www.konspekturoka.ru Куб АВСДА?В?С?Д?. Закрепление изученного материала. 1
Слайд №7
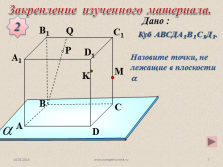
	P A B C D A1 B1 C1 D1 M K Q Назовите точки, не лежащие в плоскости ? Закрепление изученного материала. 10.03.2014 7 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 2
Слайд №8
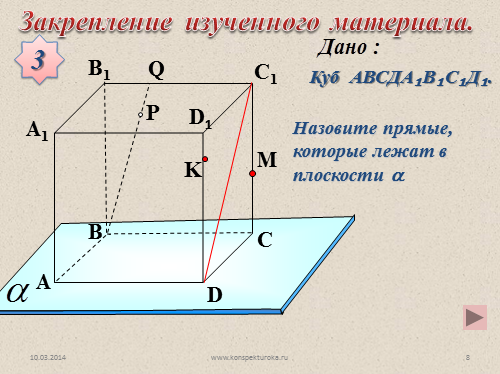
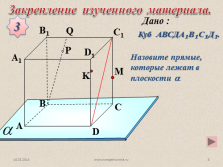
	P A B C D A1 B1 C1 D1 M K Q Назовите прямые, которые лежат в плоскости ? 10.03.2014 8 www.konspekturoka.ru Куб АВСДА?В?С?Д?. Закрепление изученного материала. 3
Слайд №9
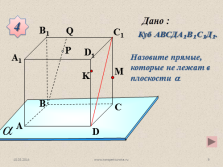
	P A B C D A1 B1 C1 D1 M K Q Назовите прямые, которые не лежат в плоскости ? 10.03.2014 9 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 4
Слайд №10
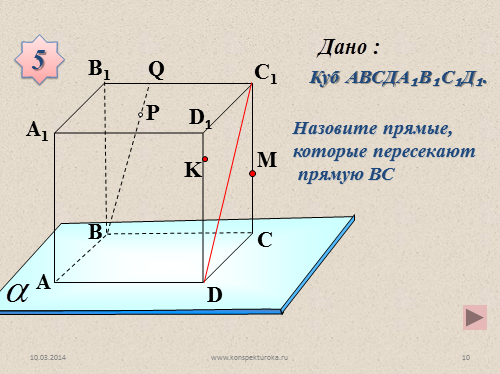
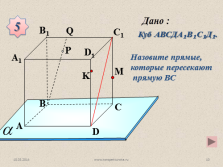
	P A B C D A1 B1 C1 D1 M K Q Назовите прямые, которые пересекают прямую ВС 10.03.2014 10 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 5
Слайд №11
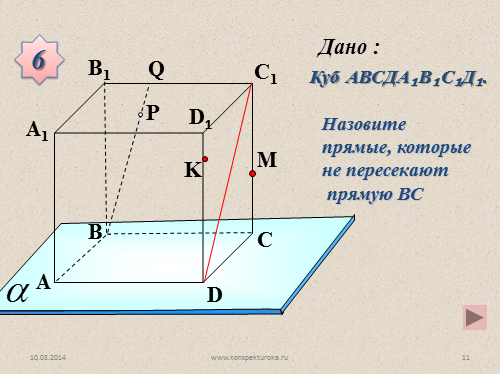
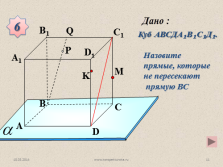
	P A B C D A1 B1 C1 D1 M K Q Назовите прямые, которые не пересекают прямую ВС 10.03.2014 11 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 6
Слайд №12
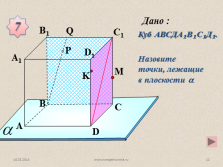
	P A B C D A1 B1 C1 D1 M K Q Назовите точки, лежащие в плоскости ? 10.03.2014 12 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 7
Слайд №13
	10.03.2014 www.konspekturoka.ru 13 Задача Две прямые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости. Лежат ли в одной плоскости все прямые, проходящие через точку М? Пусть l? ? l? = M n – произвольная прямая M ? n, n — пересекает l? и l? в точках А и К, Значит через точку А и прямую l? можно провести единственную плоскость (по теореме). Поэтому отрезки АМ, АК и КМ лежат в одной плоскости (по аксиоме А?) и прямые , которым принадлежат эти отрезки, лежат в одной плоскости. Все прямые, проходящие через М не лежат в одной плоскости. Например, прямая т. т Решение Закрепление изученного материала.
Слайд №14
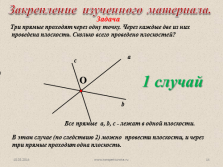
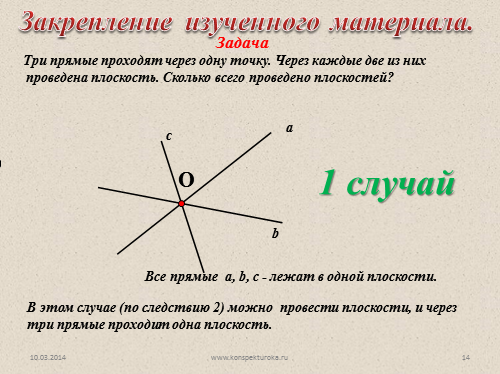
	10.03.2014 www.konspekturoka.ru 14 Задача Три прямые проходят через одну точку. Через каждые две из них проведена плоскость. Сколько всего проведено плоскостей? 1 случай Все прямые a, b, c — лежат в одной плоскости. В этом случае (по следствию 2) можно провести плоскости, и через три прямые проходит одна плоскость. Закрепление изученного материала.
Слайд №15
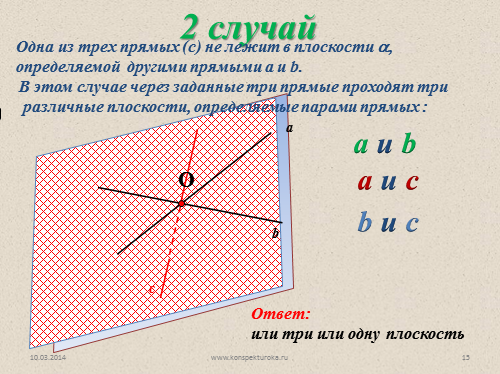
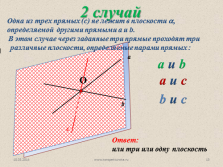
	10.03.2014 www.konspekturoka.ru 15 2 случай с Одна из трех прямых (с) не лежит в плоскости ?, определяемой другими прямыми a и b. В этом случае через заданные три прямые проходят три различные плоскости, определяемые парами прямых : a и b a и c b и c Ответ: или три или одну плоскость
Слайд №16
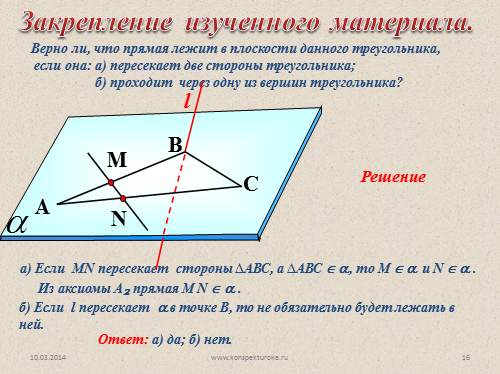
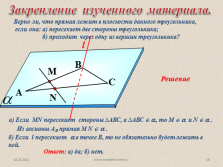
	10.03.2014 www.konspekturoka.ru 16 Верно ли, что прямая лежит в плоскости данного треугольника, если она: а) пересекает две стороны треугольника; б) проходит через одну из вершин треугольника? Решение a) Если MN пересекает стороны ?АВС, а ?АВС ? ?, то М ? ? и N ? ? . Из аксиомы А? прямая М N ? ? . б) Если l пересекает ? в точке В, то не обязательно будет лежать в ней. Ответ: а) да; б) нет. l Закрепление изученного материала.
Слайд №17
	Ответить на вопросы: 10.03.2014 17 www.konspekturoka.ru Назвать аксиомы стереометрии: — о взаимном расположении точек, — о взаимном расположении прямых, — о взаимном расположении плоскостей в пространстве. Назвать следствия из аксиом стереометрии.