Многогранники
Скачать презентацию (0.27 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Многогранники Работу выполнила ученица 11А класса Зайцева Ирина |
| Слайд №2 | |
 |
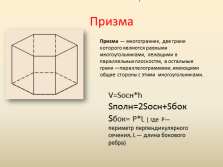Призма Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани —параллелограммами, имеющими общие стороны с этими многоугольниками. V=Sосн*h Sполн=2Sосн+Sбок Sбок= P*L ( где P— периметр перпендикулярного сечения, L — длина бокового ребра) |
| Слайд №3 | |
 |
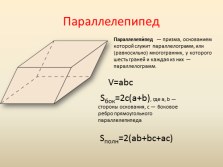Параллелепипед Параллелепи?пед — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм. V=abc Sбок=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда Sполн=2(ab+bc+ac) |
| Слайд №4 | |
 |
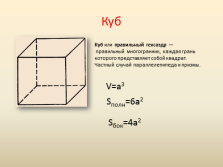Куб Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы. V=a3 Sполн=6a2 Sбок=4a2 |
| Слайд №5 | |
 |
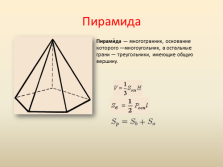Пирамида Пирами?да — многогранник, основание которого —многоугольник, а остальные грани — треугольники, имеющие общую вершину. |
| Слайд №6 | |
 |
Усеченная пирамида Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию. Sп=Sб+S1+S2 , |
| Слайд №7 | |
 |
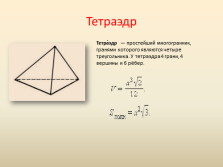Тетраэдр Тетра?эдр — простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. |
| Слайд №8 | |
 |
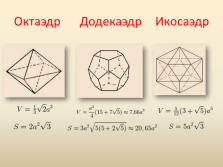Октаэдр Додекаэдр Икосаэдр |
| Слайд №9 | |
 |
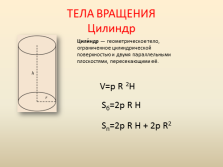ТЕЛА ВРАЩЕНИЯЦилиндр Цили?ндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. V=p R 2H Sб=2p R H Sп=2p R H + 2p R2 |
| Слайд №10 | |
 |
Конус и усеченный конус Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Усеченный конус – часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию Sб=p R L Sп=p R (R+L) Sб=p L (R+r) Sп=p L (R+r)+p R2+p r2 |
| Слайд №11 | |
 |
Шар Шар – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. S=4p R2 |
| Слайд №12 | |
 |
Шаровой сектор Шаровой сектор — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов или вокруг диаметра, не пересекающего его дуги. Sсектора= Sсегмента+ Sконуса |
| Слайд №13 | |
 |
Шаровой сегмент Шаровой сегмент — часть шара, отсекаемая какой-нибудь плоскостью. S= 2? R h |
Похожие записи:
