Многогранники

Главная Геометрия

Скачать презентацию (6.15 мб)

Слайды и текст этой презентации

Слайд №1
	Многогранники Подготовила: Ученица 10 «Б» класса Замуруева Анастасия

Слайд №2
	Пришли из Древней Греции, в них указывается число граней: «тетра» ? 4; «гекса» ? 6; «окта» ? 8; «додека» ? 12; «икоса» ? 20; «эдра» ? грань. Названия многогранников
Слайд №3
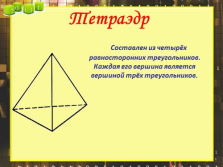	Тетраэдр Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников.
Слайд №4
	Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Октаэдр
Слайд №5
	Икосаэдр Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников.
Слайд №6
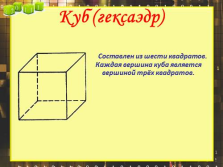	Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Куб (гексаэдр)
Слайд №7
	Правильный додекаэдр Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.
Слайд №8
	Многогранники в природе Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник. Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности. Феодария (Circjgjnia icosahtdra)
Слайд №9
	Интересно Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень — икосаэдр. Пчёлы — удивительные создания: Пчелиные соты представляют собой пространственный паркет и заполняют пространство так, что не остается просветов.
Слайд №10
	Чудо природы – кристаллы куб передает форму кристаллов поваренной соли NaCl монокристалл алюминиево-калиевых квасцов имеет форму октаэдра, кристалл сернистого колчедана FeS имеет форму додекаэдра, сернокислый натрий — тетраэдр, бор — икосаэдр. Правильные многогранники — самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников:
Слайд №11
	История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства. Из истории… Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.
Слайд №12
	Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных Платоновых тел:
Слайд №13
	Все использовали в своих философских теориях правильные многогранники. Дальнейшее развитие математики связано с именами Платона, Евклида, Архимеда, Кеплера
Слайд №14
	Титан Возрождения, живописец, скульптор, ученый и изобретатель Леонардо да Винчи (1452-1519) — символ неразрывности искусства и науки, а следовательно, закономерен его интерес к таким прекрасным, высокосимметричным объектам, как выпуклые многогранники вообще и усеченный икосаэдр в частности. Изображения Леонардо да Винчидодекаэдра методом жестких ребер (а)и методом сплошных граней(б)
Слайд №15
	Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471- 1528), в известной гравюре «Меланхолия» на переднем плане изобразил додекаэдр.
Слайд №16
	Применения икосаэдров Титульный листкниги Ж. Кузена«Книга о перспективе». Надгробный памятникв кафедральном соборе Солсбери.
Слайд №17
	Башня Сююмбике Башня Сююмбике состоит из семи ярусов, нижние ярусы представляют из себя параллелепипеды а верхние — многогранники.
Слайд №18
	Спасская башня Кремля Четыре яруса башни представляют из себя куб, многогранники и пирамиду.
Слайд №19
	Звездчатые многогранники Первые два правильных звездчатых многогранника были открыты И. Кеплером (1571-1630), а два других почти 200 лет спустя построил французский математик и механик Л. Пуансо (1777-1859). Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо.
Слайд №20