Средняя линия — 8 класс

Главная Геометрия

Скачать презентацию (0.19 мб)

Слайды и текст этой презентации

Слайд №1
	Средняя линия (8 класс)

Слайд №2
	Содержание Средняя линия треугольника Средняя линия трапеции
Слайд №3
	Средняя линия треугольника
Слайд №4
	Средняя линия треугольника. Определение: Отрезок, соединяющий середины двух сторон треугольника, называют СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.
Слайд №5
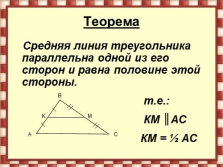	Теорема Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. т.е.: КМ ?АС КМ = ? АС A B C K M
Слайд №6
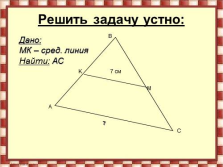	Решить задачу устно: A B C K M 7 см Дано: MК – сред. линия Найти: АС ?
Слайд №7
	Работа в парах:
Слайд №8
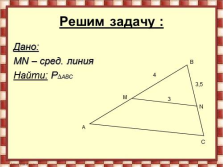	Решим задачу : Дано: MN – сред. линия Найти: P?АВС M N A B C 3 4 3,5
Слайд №9
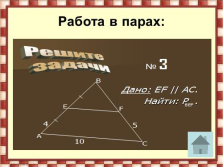	Работа в парах:
Слайд №10
	Средняя линия трапеции
Слайд №11
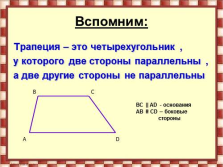	Вспомним: Трапеция – это четырехугольник , у которого две стороны параллельны , а две другие стороны не параллельны BC \|\| AD — основания AB ?? CD – боковые стороны
Слайд №12
	Средняя линия трапеции. Определение: Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. MN – средняя линия трапеции ABCD
Слайд №13
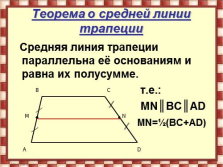	Теорема о средней линии трапеции Средняя линия трапеции параллельна её основаниям и равна их полусумме. т.е.: МN?ВС?АD МN=?(ВС+АD)
Слайд №14
	Решить устно: 6,3 см 18,7 см ?
Слайд №15
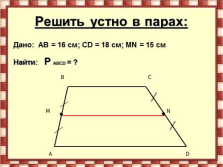	Решить устно в парах: Дано: AB = 16 см; CD = 18 см; МN = 15 см Найти: P ABCD = ?
Слайд №16
	Самостоятельная работа Задача: Средняя линия трапеции равна 5 см. Найти основания трапеции, если известно, что нижнее основание больше верхнего основания в 1,5 раз. Решение: 5 см Пусть BC = Х см тогда AD = 1.5X см BC+AD = 10 см X + 1.5X = 10 X = 4 Значит: BC = 4 см AD = 6 см
Слайд №17
	СПАСИБО ЗА УРОК !!!
Слайд №18
	Презентация разработана учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной