Трапеция и теорема Фалеса
Скачать презентацию (0.15 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Четырехугольники 8 классгеометрия Урок № 4 Трапеция 04.12.2012 1 www.konspekturoka.ru Ввести понятие трапеции и ее элементов. Познакомить с равнобедренной и прямоугольной трапецией. Рассмотреть свойства равнобедренной трапеции. |
| Слайд №2 | |
 |
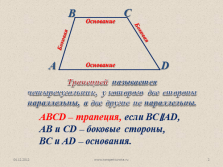
04.12.2012 www.konspekturoka.ru 2 Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. АВСD – трапеция, если ВС?AD, АВ и СD – боковые стороны, ВС и AD – основания. |
| Слайд №3 | |
 |
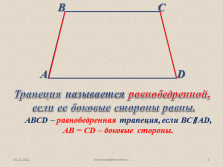
04.12.2012 www.konspekturoka.ru 3 Трапеция называется равнобедренной, если ее боковые стороны равны. АВСD – равнобедренная трапеция, если ВС? AD, АВ = СD – боковые стороны. |
| Слайд №4 | |
 |
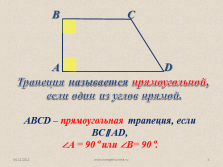
04.12.2012 www.konspekturoka.ru 4 Трапеция называется прямоугольной, если один из углов прямой. АВСD – прямоугольная трапеция, если ВС? AD, ?А = 90° или ?В= 90°. |
| Слайд №5 | |
 |
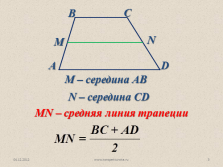
04.12.2012 www.konspekturoka.ru 5 М – середина АВ N – середина CD MN – средняя линия трапеции |
| Слайд №6 | |
 |
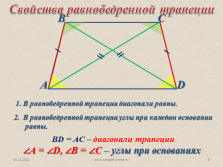
04.12.2012 www.konspekturoka.ru 6 ВD = AC – диагонали трапеции ?А = ?D, ?В = ?С – углы при основаниях Свойства равнобедренной трапеции 2. В равнобедренной трапеции углы при каждом основании равны. 1. В равнобедренной трапеции диагонали равны. |
| Слайд №7 | |
 |
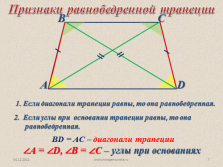
04.12.2012 www.konspekturoka.ru 7 ВD = AC – диагонали трапеции ?А = ?D, ?В = ?С – углы при основаниях Признаки равнобедренной трапеции 2. Если углы при основании трапеции равны, то она равнобедренная. 1. Если диагонали трапеции равны, то она равнобедренная. |
| Слайд №8 | |
 |
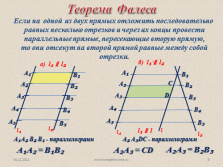
04.12.2012 www.konspekturoka.ru 8 Теорема Фалеса Если на одной из двух прямых отложить последовательно равных несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. а) l? ? l? б) l? ? l? А?А? = В?В? l? l? l? l? А?А? В? В? — параллелограмм l? ? l А? А?DC — параллелограмм А?A? = CD А?A? = В?B? |
| Слайд №9 | |
 |
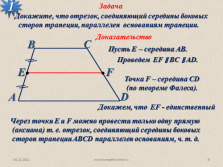
04.12.2012 www.konspekturoka.ru 9 Задача 1 Доказательство Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции. Пусть Е – середина АВ. Проведем ЕF ? BC ? AD. Точка F – середина CD (по теореме Фалеса). Докажем, что ЕF — единственный Через точки Е и F можно провести только одну прямую (аксиома) т. е. отрезок, соединяющий середины боковых сторон трапеции ABCD параллелен основаниям, ч. т. д. |
| Слайд №10 | |
 |
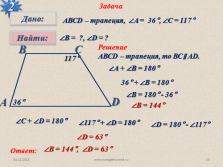
04.12.2012 www.konspekturoka.ru 10 Задача 2 АВСD – трапеция, ?A = 36°, ?C = 117° ?В = ?, ?D = ? 36° 117° Решение АВСD – трапеция, то ВС? AD. ?А + ?В = 180° 36° + ?В = 180° ?В = 180° — 36° ?В = 144° ?С + ?D = 180° ?117° + ?D = 180° ?D = 180° — ?117° ?D = 63° Ответ: ?В = 144°, ?D = 63° |
| Слайд №11 | |
 |
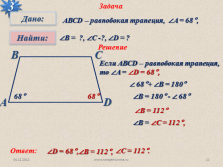
04.12.2012 www.konspekturoka.ru 11 Задача 3 АВСD – равнобокая трапеция, ?A = 68°, ?В = ?, ?С -?, ?D = ? Решение Если АВСD – равнобокая трапеция, то ?A = ?D = 68°, 68° 68° ? 68°+ ?В = 180° ?В = 180° — ? 68° ?В = 112° ?В = ?С = 112°, Ответ: |
| Слайд №12 | |
 |
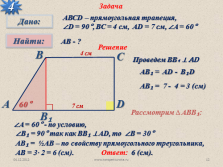
04.12.2012 www.konspekturoka.ru 12 Задача 4 АВСD – прямоугольная трапеция, ?D = 90°, BC = 4 см, AD = 7 см, ?A = 60° АВ — ? Решение Проведем ВВ? ? AD 4 см 7 см 60° AВ? = AD — B?D AВ? = 7 — 4 = 3 (см) Рассмотрим ? АBВ?: ?A = 60° — по условию, ?В? = 90° так как ВВ? ? AD, то ?В = 30° AВ? = ?АВ – по свойству прямоугольного треугольника, АВ = 3· 2 = 6 (см). Ответ: 6 (см). |
| Слайд №13 | |
 |
04.12.2012 13 Ответить на вопросы: www.konspekturoka.ru Спасибо за внимание! Какой четырехугольник называется трапецией? Как называются стороны трапеции? Какая трапеция называется прямоугольной? Равнобедренной? Сформулируйте свойства равнобедренной трапеции. Сформулируйте признаки равнобедренной трапеции. Что такое средняя линия трапеции? Свойство средней линии трапеции. |
