Теорема Пифагора

Главная Геометрия

Скачать презентацию (0.24 мб)

Слайды и текст этой презентации

Слайд №1

Разработка урока по геометрии Тема: «ТЕОРЕМА ПИФАГОРА» (8 класс)
Малахова Татьяна Викторовна

МБОУ СОШ №9 г.Грязи Липецкой области

Слайд №2
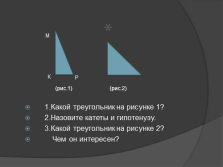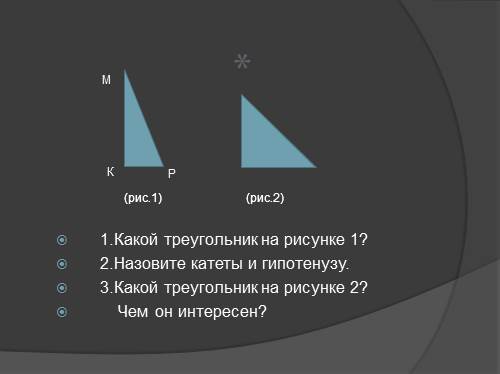
	1.Какой треугольник на рисунке 1? 2.Назовите катеты и гипотенузу. 3.Какой треугольник на рисунке 2? Чем он интересен? М Р (рис.1) (рис.2) К (рис.1) (рис.2)
Слайд №3
	В Древней Греции жил ученый Пифагор (родился он около 580г. До н.э., а умер в 500г. До н.э.). О жизни этого ученого известно немного, зато с его именем связано ряд легенд. Рассказывают, что он много путешествовал, был в Индии, Египте, Вавилоне, изучал древнюю культуру и достижения науки разных стран. Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии. В кружок принимались с большими церемониями после долгих испытаний. Каждый выступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Так, на юге Италии, которая была тогда греческой колонией, возникла так называемая пифагорейская школа. Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. В школе существовал декрет, по которому авторство всех математических работ приписывалось Пифагору. Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд, что установить о Пифагоре правду невозможно.
Слайд №4
	Задача индийского математика XII века Бхаскары На берегу реки рос тополь одинокий Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в том месте река В четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?
Слайд №5
	Постройте прямоугольные треугольники с катетами 3 и 4; 12 и 5; 6 и 8; 8 и 15 и измерить гипотенузу. Результаты занесите в таблицу. 1.Верно ли, что a+b/2=с, если это справедливо для первого и третьего случая? 2.Верно ли, что a=(b+c)/4, если это справедливо для четвертого случая? а 3 12 6 8 b 4 5 8 15 с а 3 12 6 8 b 4 5 8 15 с 5 13 10 17
Слайд №6
	доказать, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах (по сгибам бумаги). 1)Докажите справедливость теоремы для равнобедренного прямоугольного треугольника. доказать, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах в прямоугольном треугольнике (по чертежу).
Слайд №7

Слайд №8
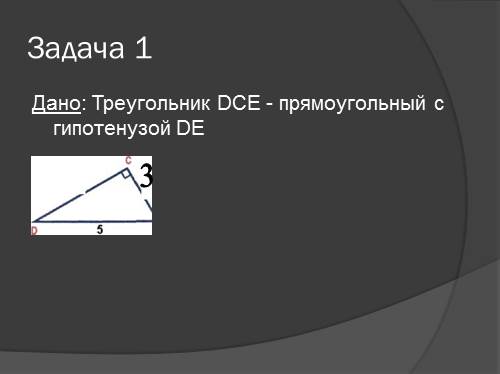
	Задача 1 Дано: Треугольник DСЕ — прямоугольный с гипотенузой DE 3
Слайд №9
	Решение Угол между курсами кораблей будет составлять 90 , отрезок, соединяющий порты назначения является гипотенузой (х) треугольника, вершинами которого являются порты назначения и главный порт. Следовательно, из условия задачи нам известны длины катетов прямоугольного треугольника. По теореме Пифагора: х = 300 + 400 = 250000, х = , х = 500. Ответ: 500 миль от восточного порта до северного.
Слайд №10
	Задача 2 Дано: Из одного порта вышли два корабля: один – на восток, другой – на север. Расстояние от главного порта до порта на востоке – 300 миль, а до порта на севере – 400 миль. Каково расстояние между двумя портами?
Слайд №11
	Решение Угол между курсами кораблей будет составлять 90 , отрезок, соединяющий порты назначения является гипотенузой (х) треугольника, вершинами которого являются порты назначения и главный порт. Следовательно, из условия задачи нам известны длины катетов прямоугольного треугольника. По теореме Пифагора: х = 300 + 400 = 250000, х = , х = 500. Ответ: 500 миль от восточного порта до северного.
Слайд №12
	Задача 3. Из китайской «Математики в девяти книгах» Дано: Имеется водоем со стороной 1 чжан = 10 чин. В центре его растет камыш который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды и какова длина камыша.
Слайд №13
	Решение 1. Пусть глубина водоёма равна х, согласно условиям задачи расстояние от камыша до берега равна половине ширины водоема, т.е. 5 чи. Треугольник, образованный камышом, растущим со дна и наклонённым к берегу, и поверхностью водоёма, является прямоугольным, в котором поверхность водоёма (5 чи) и растущий камыш (х чи) являются катетами, а наклонённый камыш((х+1) чи) является гипотенузой данного треугольника. 2.Согласно теореме Пифагора, (х+1) 2 = х2 +52 , х2+2х+1-х2 = 25, 2х = 24, x=12 Глубина водоёма составляет 12 чи, а длина камыша равна глубина водоёма + 1=13 чи. Ответ: Глубина водоёма равна 12 чи, а длина камыша – 13 чи.
Слайд №14
	Благодарю за внимание