Формула объема прямоугольного параллепипеда
Скачать презентацию (0.2 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Формула объема прямоугольного параллепипеда |
| Слайд №2 | |
 |
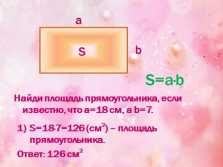Найди площадь прямоугольника, если известно, что а=18 см, а b=7. S=18·7=126 (см2) – площадь прямоугольника. Ответ: 126 см2 а b S S=a·b |
| Слайд №3 | |
 |
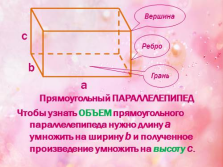Прямоугольный ПАРАЛЛЕЛЕПИПЕД Чтобы узнать ОБЪЕМ прямоугольного параллелепипеда нужно длину а умножить на ширину b и полученное произведение умножить на высоту с. Вершина Ребро Грань |
| Слайд №4 | |
 |
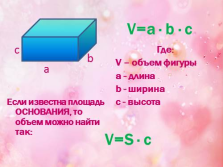Где: V – объем фигуры a — длина b — ширина c — высота V=a · b · c а b с V=S · c Если известна площадь ОСНОВАНИЯ, то объем можно найти так: |
| Слайд №5 | |
 |
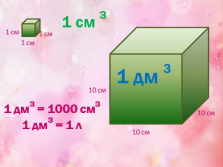1 дм3 = 1000 см3 1 дм3 = 1 л 1 см 3 1 см 1 см 1 см 10 см 10 см 10 см 1 дм 3 |
| Слайд №6 | |
 |
Существуют и другие единицы измерения объема: 1 см3 = 1000 мм3 1 м3 = 1000 дм3 1 мм 3 1 м 3 1 км 3 Переведите следующие единицы объема: 5 дм3 = … см3 8 м3 = … дм3 19 см3 = … мм3 24 дм3 = … см3 |
| Слайд №7 | |
 |
1. Найди объем прямоугольного параллелепипеда, если известно, что его длина равна 9 см, ширина – 5 см, а высота 6 см. V=9·5 ·6=270 (см3) – объем параллелепипеда. Ответ: 270 см3 2. Найди объем куба, если его длина равна 8дм. V=8·8 ·8=512 (дм3) – объем параллелепипеда. Ответ: 512 дм3 |
| Слайд №8 | |
 |
1. Площадь дна песочницы равна 400 см2, а ее высота 2 дм. Каков объем песочницы? V=400 ·2=800 (дм3) – объем песочницы. Ответ: 800 дм3 2. Известно, что объем параллелепипеда 154 м3, его ширина 2 м, а длина 11 м. Найдите высоту параллелепипеда. с=154:2:11=7 (м) – высота параллелепипеда. Ответ: 7 м |
Похожие записи:
