Исследование функций и построение графиков
Слайды и текст этой презентации
| Слайд №1 | |
 |
Павленко Надежда Васильевна учитель математики и физики НОУ «СОШ с углубленным изучением отдельных предметов имени В.Д. Чурсина» |
| Слайд №2 | |
 |
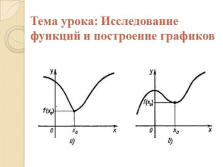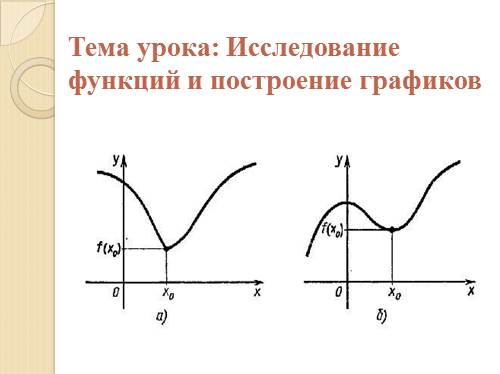
Тема урока: Исследование функций и построение графиков |
| Слайд №3 | |
 |
Цель урока: Совершенствовать умение применять полученные сведения для построения графиков функций на основе предварительного исследования |
| Слайд №4 | |
 |
Алгоритм исследования функций 1) Найти области определения и значений данной функции f. 2) Найти координаты точек пересечения графика с осями координат. 3) Найти промежутки знакопостоянства функции f. 4) Выяснит, на каких промежутках функция f возрастает, а на каких убывает. 5) Найти точки экстремума, вид экстремума (максимум или минимум) и вычислить значения f в этих точках. |
| Слайд №5 | |
 |
Область определения функции- множество значений, принимаемых независимой переменной х . Область значения функции- |
| Слайд №6 | |
 |
Функция f возрастает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2 >х1, выполнено неравенство f (х)2 > f (х1).
Функция f убывает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2 >х1, выполнено неравенство f (х)2 <f (х1). |
| Слайд №7 | |
 |
Тока х0 называется точкой минимума функции f , если для всех з из некоторой окрестности х0 выполнено неравенство f(х)>f(х0).
Тока х0 называется точкой максимума функции f , если для всех з из некоторой окрестности х0 выполнено неравенство f(х)<f(х0). |
| Слайд №8 | |
 |
|
| Слайд №9 | |
 |
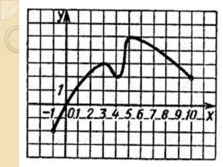
Проведите по общей схеме исследование функции 1 Вариант –рис.57 график а) 2 Вариант- рис. 57 график б) |
| Слайд №10 | |
 |
Вариант 1 Вариант 2 1. D(y)=[-8;5], E(y)=[-2;5] 1. D(y)=[-6;6], E(y)=[-2;2] 2. c Ox (1;0), (5;0) 2. c Ox (-4;0), (0;0), (4;0) 3. f(x)>0 (-8;0), (0;1) 3. f(x)>0 (-4;0), (4;6) 4. возрастает (-5;-1), (3;5) 4. возрастает(-6;-2), (2;6) 5. максимум f(-1)=5 5. максимум f(-2)=2 |
| Слайд №11 | |
 |
Постройте график функции f, если известны ее свойства Свойство функции 1 Область определения Область значений [-6;6] [-2;5] 2 Точки пересечения графика: а) с осью Ох б) с осью Оу А(-4;0). В(-2;0) С(0;2,5) 3 Промежутки знакопостоянства: а) f(x)>0 б) f(x)<0 [-6;-4). (-2;6] (-4;-2) 4 Промежутки : а) возрастания б) убывания [-3;1], [4;6] [-6;-3], [1;4] 5 Точки максимума, максимум функции Точки минимума, минимум функции (1)=3 (-3)=-2; (4)=1 6 Дополнительные точки графика f(-6)=3; f(6)=5 |
| Слайд №12 | |
 |
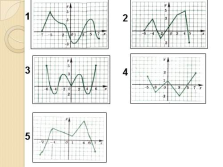1 2 3 4 5 |
| Слайд №13 | |
 |
Итог урока 5 плюсов – оценка «5» 4 плюса- оценка «4» 3 плюса –оценка «3» |
| Слайд №14 | |
 |
Домашнее задание Задание- практическое: пункт 6 читать; №94 (б, г); №95 (в, г); №96 (б); №97 (в) |
| Слайд №15 | |
 |
Задание аналитическое: Отыщите функцию, среди предложенных, исходя из её «автобиографии»: Я – функция сложная, это известно, Ещё расскажу, если Вам интересно, Что точку разрыва и корень имею, И есть интервал, где расти не посмею. Во всём остальном положительна, право. И это конечно не ради забавы. Для чисел больших я стремлюсь к единице. Найдите меня среди прочих в таблице. |
| Слайд №16 | |
 |
Поделитесь своим впечатлением 1)Что вы сегодня изучали на уроке? 2) Какие задания вызвали у вас затруднения? 3) Какие задания вам понравились? 4)Какие знания математики пригодились вам на уроке? |
| Слайд №17 | |
 |
Спасибо за урок! |
| Слайд №18 | |
 |
Список литературы: 1. Учебник А.Н. Колмогоров «Алгебра и начала анализа. 10-11 класс». 2. Денищева Л.О. Седова Е.А. Дидактические материалы по алгебре и началам анализа 10-11 класс. 3. Кузнецова Г.М. Программа для общеобразовательных школ, гимназий. Математика., 2000. 4. Ивлев Б.М. Дидактические материалы по алгебре и началам анализа 10 класс. М. |
