Построение графиков более сложных функций. Построение уравнения.
Скачать презентацию (0.19 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Линейная функция 7 классалгебра Уроки № 11-12 Построение графиков более сложных функций. Построение уравнения (факультативные занятия). 08.07.2012 1 www.konspekturoka.ru |
| Слайд №2 | |
 |
Цели: 08.07.2012 Получить навыки построения сложных графиков. Дать простейшие представления о графиках уравнений. Научить строить графики. 2 www.konspekturoka.ru |
| Слайд №3 | |
 |
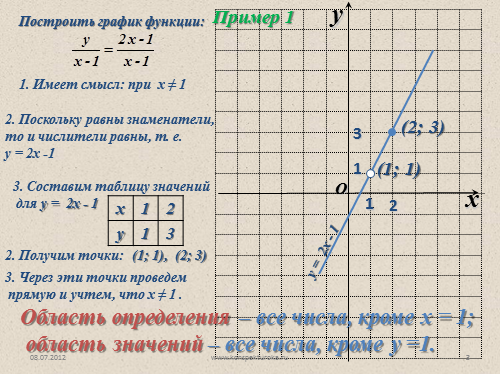
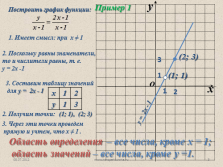
08.07.2012 www.konspekturoka.ru 3 1. Имеет смысл: при х ? 1 2. Поскольку равны знаменатели, то и числители равны, т. е. у = 2х -1 3 1 (1; 1) (2; 3) у = 2х — 1 3. Составим таблицу значений для у = 2х — 1 2. Получим точки: (1; 1), (2; 3) 3. Через эти точки проведем прямую и учтем, что х ? 1 . Область определения – все числа, кроме х = 1; область значений – все числа, кроме у =1. |
| Слайд №4 | |
 |
08.07.2012 www.konspekturoka.ru 4 Имеет смысл: при х — 1 ? 0 (х ? 1) х + 2 ? 0 (х ? -2) Из обеих частей вычитаем: Получим: Умножим обе части на (х + 2): Получим: у + х = х + 2, или у = 2 При любом значении аргумента х значение функции равно одной и той же величине у = 2. Точки А(-1; 2), В(2; 2) принадлежат графику функции. -2 (-2; 2) (1; 2) у = 2 Учтем: при х ? 1, х ? -2 Область определения – все числа, кроме х = 1, х = -2; область значений – число у = 2. |
| Слайд №5 | |
 |
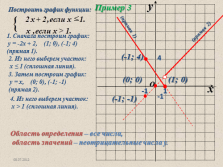
08.07.2012 1. Сначала построим график: у = -2х + 2, (1; 0), (-1; 4) (прямая 1). 2. Из него выберем участок: х ? 1 (сплошная линия). 1 (1; 0) (-1; 4) (прямая 1) 3. Затем построим график: у = х, (0; 0), (-1; -1) (прямая 2). 4. Из него выберем участок: х > 1 (сплошная линия). (-1; -1) (0; 0) (прямая 2) Область определения – все числа, область значений – неотрицательные числа у. |
| Слайд №6 | |
 |
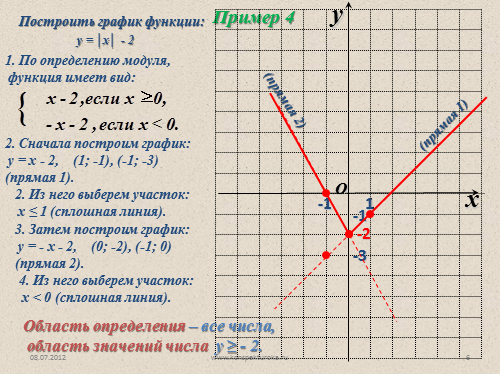
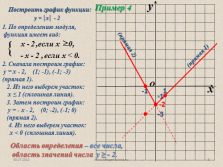
08.07.2012 www.konspekturoka.ru 6 у = ?х? — 2 2. Сначала построим график: у = х — 2, (1; -1), (-1; -3) (прямая 1). 2. Из него выберем участок: х ? 1 (сплошная линия). (прямая 1) -2 3. Затем построим график: у = — х — 2, (0; -2), (-1; 0) (прямая 2). (прямая 2) 4. Из него выберем участок: х < 0 (сплошная линия). Область определения – все числа, область значений числа у ? — 2. |
| Слайд №7 | |
 |
08.07.2012 www.konspekturoka.ru 7 Построение уравнения Вспомним! Функциональные зависимости (функции)- зависимости в которых каждому значению переменной х соответствует только одно значение переменной у. В математике встречаются и такие зависимости между переменными х и у, при которых одному значению х может соответствовать более одного значения у. В этом случае говорят о графике уравнения. |
| Слайд №8 | |
 |
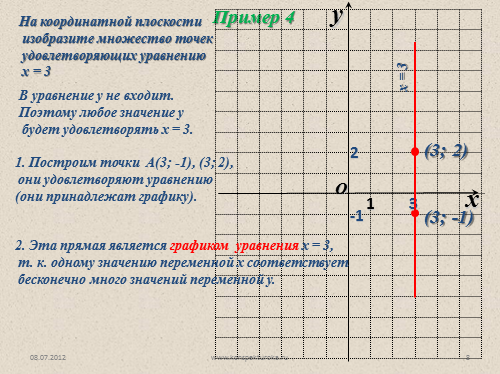
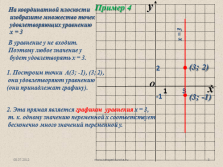
08.07.2012 www.konspekturoka.ru 8 В уравнение у не входит. Поэтому любое значение у будет удовлетворять х = 3. 1. Построим точки А(3; -1), (3; 2), они удовлетворяют уравнению (они принадлежат графику). (3; -1) х = 3 (3; 2) 2. Эта прямая является графиком уравнения х = 3, т. к. одному значению переменной х соответствует бесконечно много значений переменной у. |
| Слайд №9 | |
 |
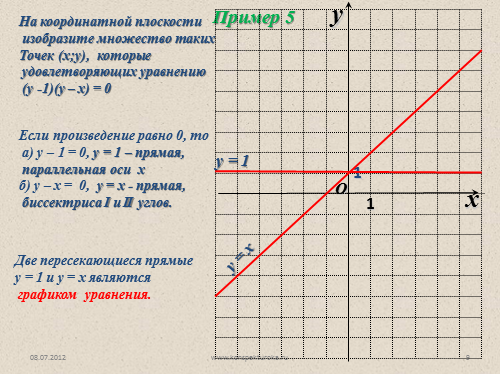
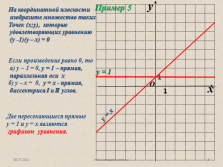
08.07.2012 www.konspekturoka.ru 9 Если произведение равно 0, то а) у – 1 = 0, у = 1 – прямая, параллельная оси х б) у – х = 0, у = х — прямая, биссектриса I и II углов. 1 у = 1 у = х Две пересекающиеся прямые у = 1 и у = х являются графиком уравнения. |
| Слайд №10 | |
 |
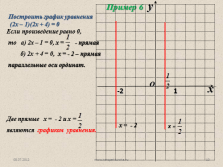
08.07.2012 www.konspekturoka.ru 10 Построить график уравнения (2х – 1)(2х + 4) = 0 Пример 6 х = — 2 |
| Слайд №11 | |
 |
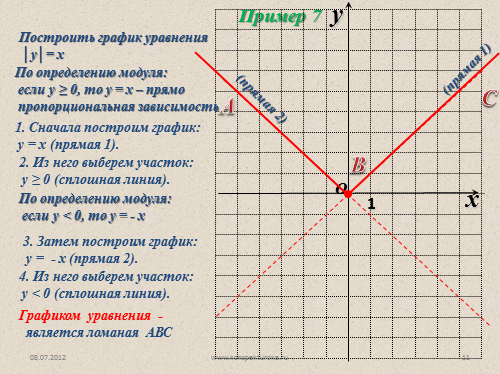
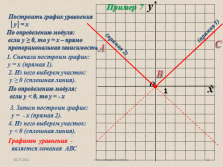
08.07.2012 www.konspekturoka.ru 11 Построить график уравнения ?у?= х Пример 7 По определению модуля: если у ? 0, то у = х – прямо пропорциональная зависимость 1. Сначала построим график: у = х (прямая 1). (прямая 1) 2. Из него выберем участок: у ? 0 (сплошная линия). 3. Затем построим график: у = — х (прямая 2). (прямая 2) 4. Из него выберем участок: у < 0 (сплошная линия). Графиком уравнения — является ломаная АВС По определению модуля: если у < 0, то у = — х |
| Слайд №12 | |
 |
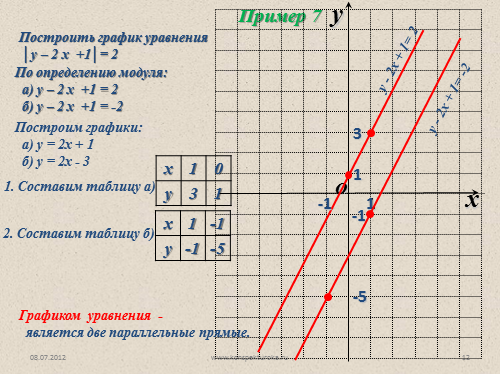
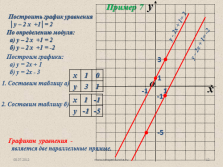
08.07.2012 www.konspekturoka.ru 12 Построить график уравнения ?у – 2 x +1?= 2 Пример 7 По определению модуля: а) у – 2 x +1 = 2 б) у – 2 x +1 = -2 Построим графики: а) у = 2х + 1 б) у = 2х — 3 1. Составим таблицу а) у — 2х + 1= 2 2. Составим таблицу б) у — 2х + 1= -2 Графиком уравнения — является две параллельные прямые. |
| Слайд №13 | |
 |
08.07.2012 13 www.konspekturoka.ru Спасибо за внимание! |
