Описанная окружность
Скачать презентацию (0.03 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Описанная окружность |
| Слайд №2 | |
 |
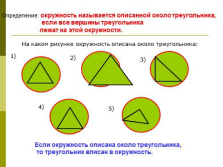Определение: окружность называется описанной около треугольника, если все вершины треугольника лежат на этой окружности. Если окружность описана около треугольника, то треугольник вписан в окружность. |
| Слайд №3 | |
 |
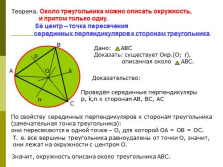Теорема. Около треугольника можно описать окружность, и притом только одну. Её центр – точка пересечения серединных перпендикуляров к сторонам треугольника. Доказательство: Проведём серединные перпендикуляры p, k,n к сторонам АВ, ВС, АС По свойству серединных перпендикуляров к сторонам треугольника (замечательная точка треугольника): они пересекаются в одной точке – О, для которой ОА = ОВ = ОС. Т. е. все вершины треугольника равноудалены от точки О, значит, они лежат на окружности с центром О. Значит, окружность описана около треугольника АВС. |
| Слайд №4 | |
 |
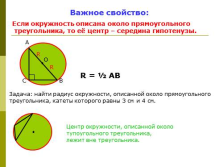Важное свойство: Если окружность описана около прямоугольного треугольника, то её центр – середина гипотенузы. R = ? AB Задача: найти радиус окружности, описанной около прямоугольного треугольника, катеты которого равны 3 см и 4 см. |
| Слайд №5 | |
 |
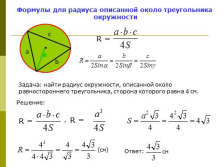Формулы для радиуса описанной около треугольника окружности Задача: найти радиус окружности, описанной около равностороннего треугольника, сторона которого равна 4 см. Решение: |
| Слайд №6 | |
 |
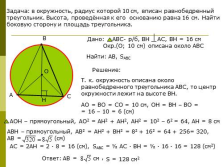Задача: в окружность, радиус которой 10 см, вписан равнобедренный треугольник. Высота, проведённая к его основанию равна 16 см. Найти боковую сторону и площадь треугольника. Решение: Т. к. окружность описана около равнобедренного треугольника АВС, то центр окружности лежит на высоте ВН. АО = ВО = СО = 10 см, ОН = ВН – ВО = = 16 – 10 = 6 (см) АС = 2АН = 2 · 8 = 16 (см), SАВС = ? АС · ВН = ? · 16 · 16 = 128 (см2) |
| Слайд №7 | |
 |
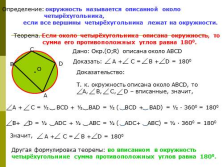Определение: окружность называется описанной около четырёхугольника, если все вершины четырёхугольника лежат на окружности. Теорема. Если около четырёхугольника описана окружность, то сумма его противоположных углов равна 1800. Доказательство: Другая формулировка теоремы: во вписанном в окружность четырёхугольнике сумма противоположных углов равна 1800. |
| Слайд №8 | |
 |
Обратная теорема: если сумма противоположных углов четырёхугольника равна 1800, то около него можно описать окружность. Доказательство: № 729 (учебник) Вокруг какого четырёхугольника нельзя описать окружность? |
| Слайд №9 | |
 |
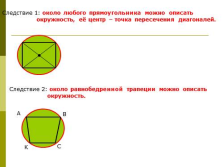Следствие 1: около любого прямоугольника можно описать окружность, её центр – точка пересечения диагоналей. Следствие 2: около равнобедренной трапеции можно описать окружность. |
| Слайд №10 | |
 |
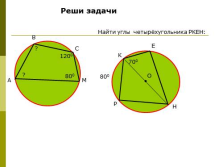Реши задачи |
Похожие записи:
