Линейное уравнение с одной переменной — Математические модели
Скачать презентацию (2.51 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Интегрированный урок по темам «Линейное уравнение с одной переменной. Математические модели.» |
| Слайд №2 | |
 |
Научиться можно Только тому, Что любишь Иоганн гёте |
| Слайд №3 | |
 |
Правила «Космических гонок» |
| Слайд №4 | |
 |
1 этап Найдите число, противоположное корню уравнения (2 + 3х) – (4х – 7) = 10 |
| Слайд №5 | |
 |
Ответ (2 + 3х) – (4х – 7) = 10 2 + 3х – 4х + 7 = 10 3х – 4х = 10 – 2 – 7 х = 1 х = — 1 Число, противоположное корню: 1 |
| Слайд №6 | |
 |
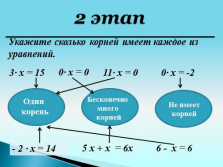Укажите сколько корней имеет каждое из уравнений. — 2 ? x = 14 0? x = 0 11? x = 0 0? x = -2 Один корень Бесконечно много корней Не имеет корней 5 x + х = 6х 3? x = 15 6 — x = 6 2 этап |
| Слайд №7 | |
 |
3 этап х+9 3 ? х 5 =1 Решите уравнение: |
| Слайд №8 | |
 |
Ответ 5(х + 9) – 3х = 15 5х + 45 – 3х = 15 5х – 3х = 15 – 45 2х = -30 х = -15 Ответ: -15 | ·15 |
| Слайд №9 | |
 |
Во время соревнований из пункта А и пункта Б навстречу друг другу выехали 2 велосипедиста. Скорость одного из них на 2 км/ч больше, чем скорость второго. Найти скорость каждого велосипедиста, если расстояние между пунктами 160 км, а встретились они через 5 часов. 4 этап |
| Слайд №10 | |
 |
5х + 5(х + 2) = 160 5х + 5х + 10 = 160 5х + 5х = 160 – 10 10х = 150 х = 15 Скорость первого 15 км/ч, скорость второго 17 км/ч. Ответ |
| Слайд №11 | |
 |
Моторная лодка за 2 ч по течению реки проплывает такое же расстояние, как за 3 часа против течения реки. Найдите собственную скорость лодки, если скорость течения реки равна 3 км/ч. 5 этап |
| Слайд №12 | |
 |
2(х + 3) = 3(х – 3) 2х + 6 = 3х – 9 9 + 6 = 3х – 2х х = 15 Скорость моторной лодки 15 км/ч. Ответ |
