Слайды и текст этой презентации
| Слайд №1 |
 |
Подготовка К ЕГЭ — 2016Задача В9
Базовый и профильный уровни
Учитель математики
ГБОУ гимназия №1 города Похвистнево
Самарской области
Антонова Галина Васильевна |
| Слайд №2 |
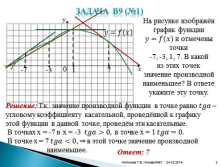 |
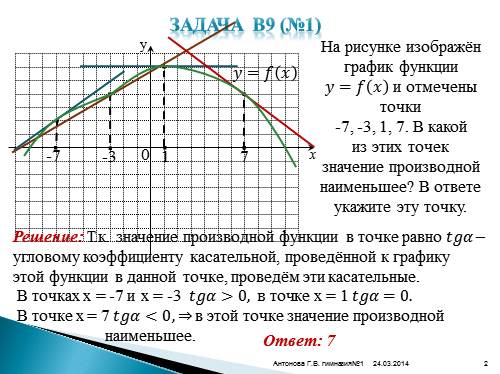
Задача В9 (№1)
y
x
?
?
?
?
?
?
?
?
На рисунке изображён график функции ????=???? ???? и отмечены точки
-7, -3, 1, 7. В какой
из этих точек значение производной наименьшее? В ответе укажите эту точку.
-7
-3
0
1
7
В точках х = -7 и х = -3 ????????????>0, в точке х = 1 ????????????=0.
В точке х = 7 ????????????<0, ? в этой точке значение производной
наименьшее.
Ответ: 7
Решение: Т.к. значение производной функции в точке равно ???????????? – угловому коэффициенту касательной, проведённой к графику этой функции в данной точке, проведём эти касательные.
24.03.2016
Антонова Г.В. гимназия№1
2
????=???? ???? |
| Слайд №3 |
 |
24.03.2016
Антонова Г.В. гимназия№1
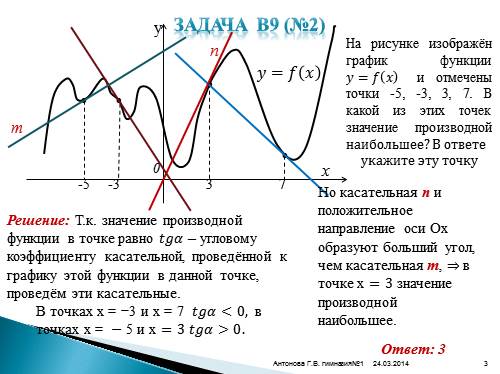
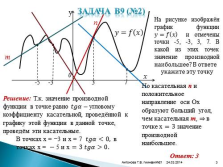
Задача В9 (№2)На рисунке изображён график функции ????=???? ???? и отмечены точки -5, -3, 3, 7. В какой из этих точек значение производной наибольшее?В ответе
укажите эту точку
Решение: Т.к. значение производной функции в точке равно ???????????? – угловому коэффициенту касательной, проведённой к графику этой функции в данной точке, проведём эти касательные.
Но касательная n и положительное направление оси Ох образуют больший угол, чем касательная m, ? в точке х=3 значение производной
наибольшее.
m
n
В точках х = ?3 и х = 7 ????????????0.
Ответ: 3
3
????=???? ???? |
| Слайд №4 |
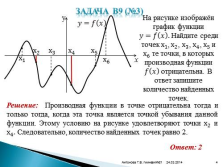 |
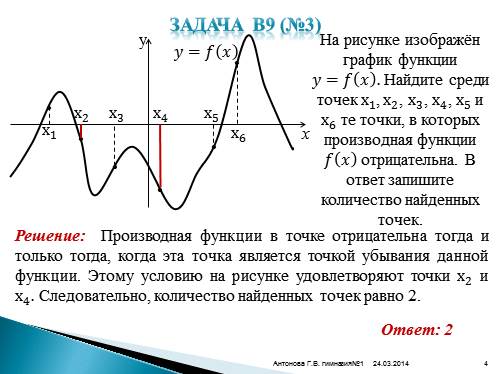
Задача В9 (№3)
На рисунке изображён график функции ????=???? ???? . Найдите среди точек х 1 , х 2 , х 3 , х 4 , х 5 и х 6 те точки, в которых производная функции ???? ???? отрицательна. В ответ запишите количество найденных точек.
Решение: Производная функции в точке отрицательна тогда и только тогда, когда эта точка является точкой убывания данной функции. Этому условию на рисунке удовлетворяют точки x 2 и x 4 . Следовательно, количество найденных точек равно 2.
Ответ: 2
24.03.2016
Антонова Г.В. гимназия№1
4 |
| Слайд №5 |
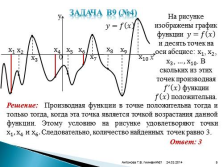 |
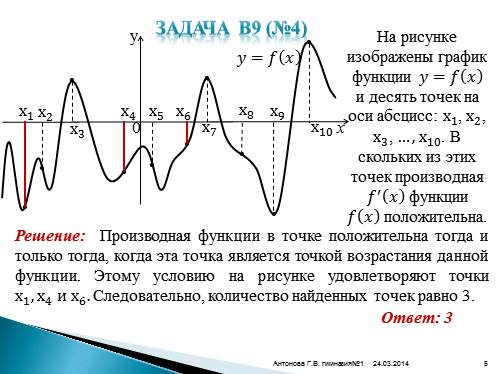
Задача В9 (№4)
24.03.2016
Антонова Г.В. гимназия№1
На рисунке изображены график функции ????=???? ???? и десять точек на оси абсцисс: х 1 , х 2 , х 3 , …, х 10 . В скольких из этих точек производная ???? ? ???? функции ???? ???? положительна.
Решение: Производная функции в точке положительна тогда и только тогда, когда эта точка является точкой возрастания данной функции. Этому условию на рисунке удовлетворяют точки x 1 , x 4 и х 6 . Следовательно, количество найденных точек равно 3.
Ответ: 3
5
????=???? ???? |
| Слайд №6 |
 |
24.03.2016
Антонова Г.В. гимназия№1
6
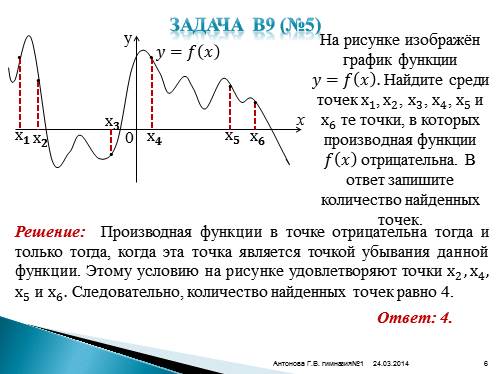
Задача В9 (№5)Решение: Производная функции в точке отрицательна тогда и только тогда, когда эта точка является точкой убывания данной функции. Этому условию на рисунке удовлетворяют точки x 2 , x 4 , x 5 и x 6 . Следовательно, количество найденных точек равно 4.
На рисунке изображён график функции ????=???? ???? . Найдите среди точек х 1 , х 2 , х 3 , х 4 , х 5 и х 6 те точки, в которых производная функции ???? ???? отрицательна. В ответ запишите количество найденных точек.
Ответ: 4. |
| Слайд №7 |
 |
24.03.2016
Антонова Г.В. гимназия№1
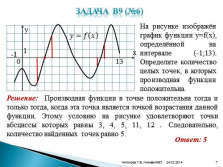
Задача В9 (№6)7
y
x
0
1
-1
13
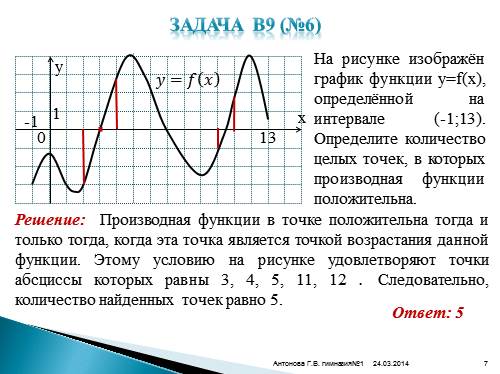
На рисунке изображён график функции y=f(x), определённой на интервале (-1;13). Определите количество целых точек, в которых производная функции положительна.
?
Решение: Производная функции в точке положительна тогда и только тогда, когда эта точка является точкой возрастания данной функции. Этому условию на рисунке удовлетворяют точки абсциссы которых равны 3, 4, 5, 11, 12 . Следовательно, количество найденных точек равно 5.
Ответ: 5
????=???? ???? |
| Слайд №8 |
 |
Этому условию на рисунке удовлетворяют точки x 2 и x 4 . Следовательно, количество найденных точек равно 2.
24.03.2016
Антонова Г.В. гимназия№1
8
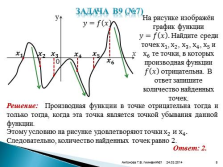
Задача В9 (№7)
y
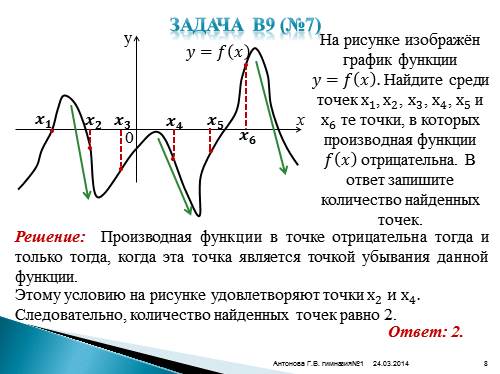
На рисунке изображён график функции ????=???? ???? . Найдите среди точек х 1 , х 2 , х 3 , х 4 , х 5 и х 6 те точки, в которых производная функции ???? ???? отрицательна. В ответ запишите количество найденных точек.
Решение: Производная функции в точке отрицательна тогда и только тогда, когда эта точка является точкой убывания данной функции.
Ответ: 2. |
| Слайд №9 |
 |
24.03.2016
Антонова Г.В. гимназия№1
9
y
x
Задача В9 (№8)????=???? ????
0
•
•
•
•
•
•
•
На рисунке изображён график функции y=f(x), определённой на интервале (-1;13). Определите количество целых точек, в которых производная функции положительна.
Ответ: 2.
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????
Решение: Производная функции в точке положительна тогда и только тогда, когда эта точка является точкой возрастания данной функции. Этому условию на рисунке удовлетворяют точки x 3 и х 6 . Следовательно, количество найденных точек равно 2. |
| Слайд №10 |
 |
24.03.2016
Антонова Г.В. гимназия№1
2
8
m
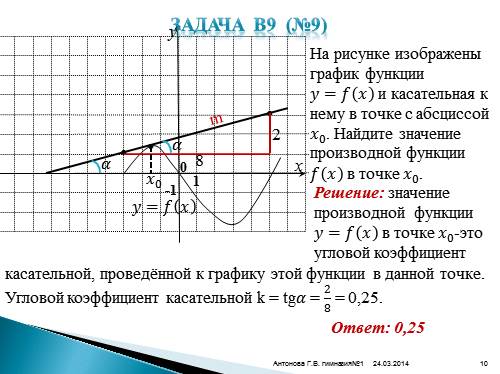
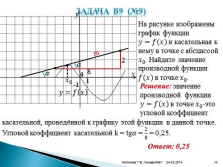
На рисунке изображены график функции ????=???? ???? и касательная к нему в точке с абсциссой ???? 0 . Найдите значение производной функции ???? ???? в точке ???? 0 .
0
???? 0
10
Решение: значение производной функции ????=???? ???? в точке ???? 0 -это угловой коэффициент
касательной, проведённой к графику этой функции в данной точке. Угловой коэффициент касательной k = tg???? = 2 8 = 0,25.????
????
Ответ: 0,25
????=???? ???? |
| Слайд №11 |
 |
24.03.2016
Антонова Г.В. гимназия№1
11
???? 0
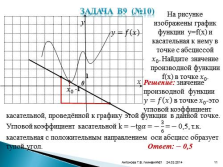
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой ???? 0 . Найдите значение производной функции f(x) в точке ???? 0 .
Решение: значение производной функции ????=???? ???? в точке ???? 0 -это угловой коэффициент
касательной, проведённой к графику этой функции в данной точке. Угловой коэффициент касательной k = ?tg???? = ? 3 6 = ? 0,5, т.к. касательная с положительным направлением оси абсцисс образует тупой угол.Ответ: ? 0,5
????=???? ????
0 |
| Слайд №12 |
 |
????
24.03.2016
Антонова Г.В. гимназия№1
12
Задача В9 (№11)y
x
???? ????
0
1
-1
На рисунке изображены график функции ????=???? ???? и касательная к нему в точке с абсциссой ???? 0 . Найдите значение производной функции ???? ???? в точке ???? 0 .
Решение: значение производной функции ????=???? ???? в точке ???? 0 -это угловой коэффициент касательной, проведённой к графику этой функции в данной точке. Угловой коэффициент касательной k = tg???? = 8 10 = 0,8, т.к. касательная с положительным направлением оси абсцисс образует острый угол.8
10
Ответ: 0,8.
x
????=???? ????
•
• |
| Слайд №13 |
 |
24.03.2016
Антонова Г.В. гимназия№1
13
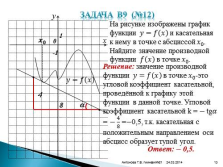
Задача В9 (№12)0
???? ????
x
1
-1
y
На рисунке изображены график функции ????=???? ???? и касательная к нему в точке с абсциссой ???? 0 . Найдите значение производной функции ???? ???? в точке ???? 0 .
Решение: значение производной функции ????=???? ???? в точке ???? 0 -это угловой коэффициент касательной, проведённой к графику этой функции в данной точке. Угловой коэффициент касательной k = ? tg???? = ? 4 8 =?0,5, т.к. касательная с положительным направлением оси абсцисс образует тупой угол.????
4
8
Ответ: ? 0,5.
????=???? ????
•
• |
| Слайд №14 |
 |
24.03.2016
Антонова Г.В. гимназия№1
14
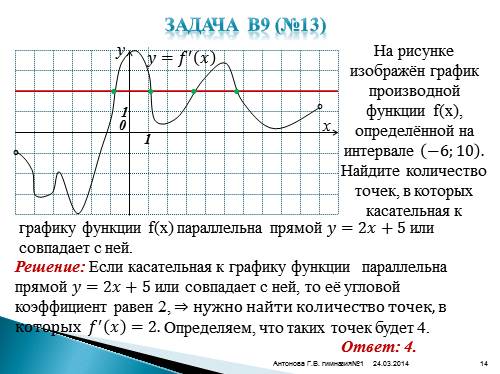
Задача В9 (№13)y
x
0
1
1
????=???? ? ????
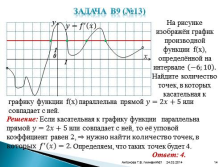
На рисунке изображён график производной функции f(x), определённой на интервале ?6;10 . Найдите количество точек, в которых касательная к
°
°
графику функции f(x) параллельна прямой ????=2????+5 или совпадает с ней.Решение: Если касательная к графику функции параллельна прямой ????=2????+5 или совпадает с ней, то её угловой коэффициент равен 2, ? нужно найти количество точек, в которых ???? ? ???? =2.
•
•
•
•
Определяем, что таких точек будет 4.
Ответ: 4. |
| Слайд №15 |
 |
24.03.2016
Антонова Г.В. гимназия№1
15
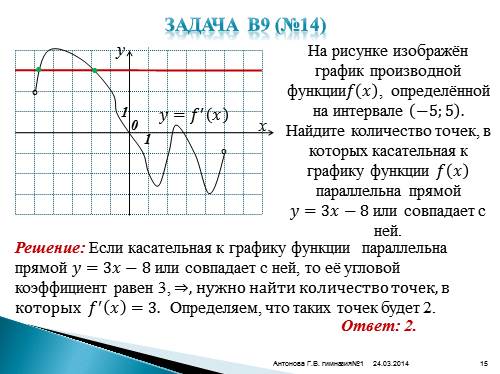
Задача В9 (№14)y
x
0
1
1
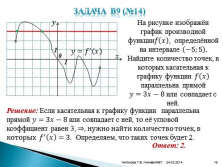
На рисунке изображён график производной функции???? ???? , определённой на интервале ?5;5 . Найдите количество точек, в которых касательная к графику функции ???? ???? параллельна прямой ????=3?????8 или совпадает с ней.
Решение: Если касательная к графику функции параллельна прямой ????=3?????8 или совпадает с ней, то её угловой коэффициент равен 3, ?, нужно найти количество точек, в которых ???? ? ???? =3.
°
°
•
•
????=???? ? ????
Определяем, что таких точек будет 2.Ответ: 2. |
| Слайд №16 |
 |
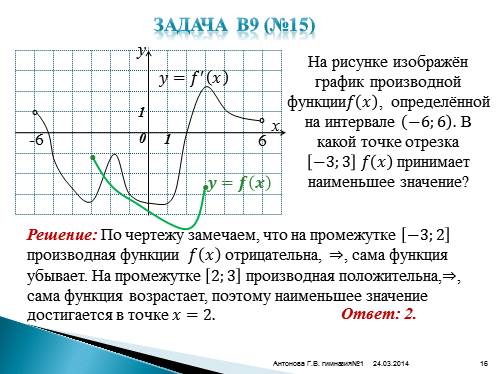
Задача В9 (№15)
24.03.2016
Антонова Г.В. гимназия№1
16
°
°
y
x
????=???? ? ????
0
1
1
-6
6
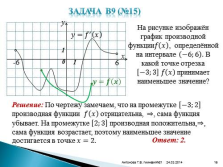
На рисунке изображён график производной функции???? ???? , определённой на интервале ?6;6 . В какой точке отрезка ?3;3 ???? ???? принимает наименьшее значение?
Решение: По чертежу замечаем, что на промежутке ?3;2 производная функции ???? ???? отрицательна, ?, сама функция убывает. На промежутке 2;3 производная положительна,?, сама функция возрастает, поэтому наименьшее значение достигается в точке ????=2.
Ответ: 2.
????=???? ????
•
• |
| Слайд №17 |
 |
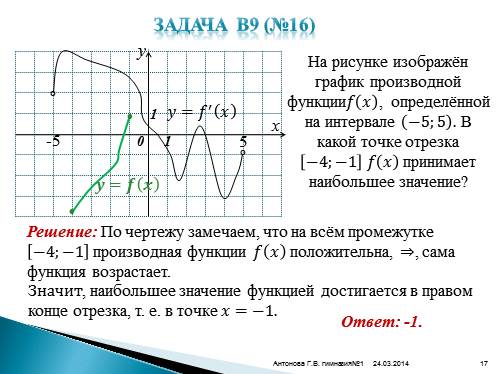
Значит, наибольшее значение функцией достигается в правом конце отрезка, т. е. в точке ????=?1.
24.03.2016
Антонова Г.В. гимназия№1
17
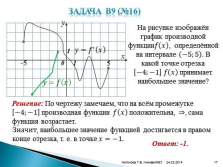
Задача В9 (№16)
°
°
????=???? ? ????
На рисунке изображён график производной функции???? ???? , определённой на интервале ?5;5 . В какой точке отрезка ?4;?1 ???? ???? принимает наибольшее значение?
Решение: По чертежу замечаем, что на всём промежутке ?4;?1 производная функции ???? ???? положительна, ?, сама функция возрастает.
Ответ: -1.
????=???? ????
•
• |
| Слайд №18 |
 |
24.03.2016
Антонова Г.В. гимназия№1
18
Задача В9 (№17)17а) Прямая ????=6????+9 параллельна касательной к графику функции ????= ???? 2 +7?????6. Найдите абсциссу точки касания
Решение: Значение производной функции в точке касания равно
угловому коэффициенту касательной, которая параллельна прямой
????=6????+9, т.е. ???? ? =6 ? 2????+7=6,
????=?0,5.
Ответ: ? 0,5.
17б) Прямая ????=?4?????8 является касательной к графику функции ????= ???? 3 ?3 ???? 2 ??????9. Найдите абсциссу точки касанияРешение: Значение производной функции в точке касания равно
угловому коэффициенту касательной, т.е. ???? ? =?4 ?
3???? 2 ?6?????1=?4? 3???? 2 ?6????+3=0 ? ?????1 2 =0, ????=1.
Ответ: ????. |
| Слайд №19 |
 |
Вычислим значения функции в этих точках и проверим, удовлетворяют ли они уравнению касательной :
1) ???? 2 = 2 3 ?4? 2 2 +9?2+14=24 и 5?2+14=24 ?
????=2 удовлетворяет,
2) ???? 2 3 = 2 3 3 ?4? 2 3 2 +9? 2 3 +14= 824 27 , но 824 27 ?5? 2 3 +14?
????= 2 3 не удовлетворяет. Т.е. искомая абсцисса точки
касания =2.24.03.2016
Антонова Г.В. гимназия№1
19
Задача В9 (№17)17в) Прямая ????=5????+14 является касательной к графику функции ????= ???? 3 ?4 ???? 2 +9????+14. Найдите абсциссу точки касания
Решение: Значение производной функции в точке касания равно
угловому коэффициенту касательной, т.е. ???? ? =5 ?
3???? 2 ?8????+9=5, 3???? 2 ?8????+4=0, т.е. ????=2; 2 3 .
Ответ: 2. |
| Слайд №20 |
 |
24.03.2016
Антонова Г.В. гимназия№1
20
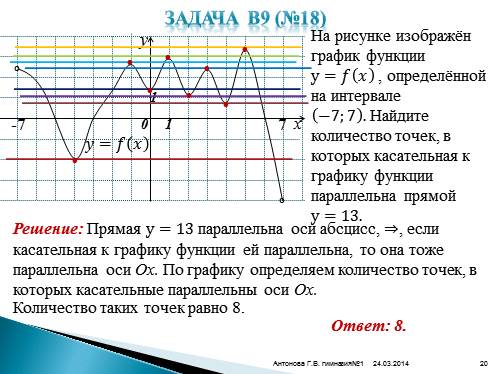
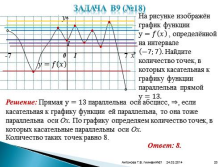
Задача В9 (№18)x
На рисунке изображён график функции y=???? ???? , определённой на интервале ?7;7 . Найдите количество точек, в которых касательная к графику функции параллельна прямой y=13.
Решение: Прямая y=13 параллельна оси абсцисс, ?, если касательная к графику функции ей параллельна, то она тоже параллельна оси Ох. По графику определяем количество точек, в которых касательные параллельны оси Ох.
•
•
•
•
•
•
•
•
Количество таких точек равно 8.
Ответ: 8.
????=???? ???? |
| Слайд №21 |
 |
24.03.2016
Антонова Г.В. гимназия№1
21
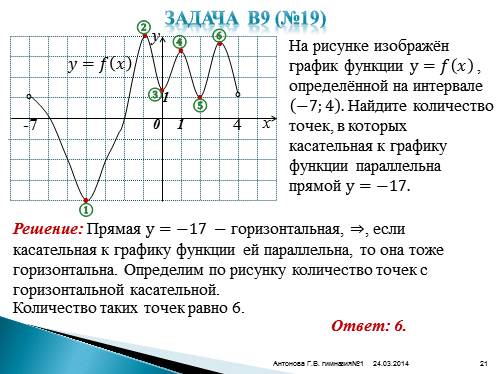
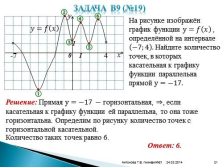
Задача В9 (№19)????=???? ????
x
На рисунке изображён график функции y=???? ???? , определённой на интервале ?7;4 . Найдите количество точек, в которых касательная к графику функции параллельна прямой y=?17.
Решение: Прямая y=?17 ? горизонтальная, ?, если касательная к графику функции ей параллельна, то она тоже горизонтальна. Определим по рисунку количество точек с горизонтальной касательной.
Количество таких точек равно 6.
•
•
•
•
•
•
?
?
?
?
?
?
Ответ: 6. |
| Слайд №22 |
 |
?
?
24.03.2016
Антонова Г.В. гимназия№1
22
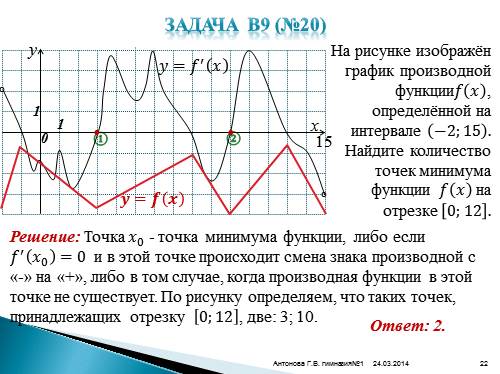
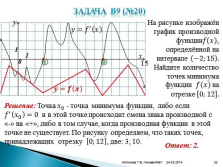
Задача В9 (№20)На рисунке изображён график производной функции???? ???? , определённой на интервале ?2;15 . Найдите количество точек минимума функции ???? ???? на отрезке 0;12 .
15
????=???? ? ????
Решение: Точка ???? 0 — точка минимума функции, либо если ???? ? ???? 0 =0 и в этой точке происходит смена знака производной с «-» на «+», либо в том случае, когда производная функции в этой точке не существует. По рисунку определяем, что таких точек, принадлежащих отрезку 0;12 , две: 3; 10.
Ответ: 2.
•
•
°
°
????=???? ???? |
| Слайд №23 |
 |
24.03.2016
Антонова Г.В. гимназия№1
23
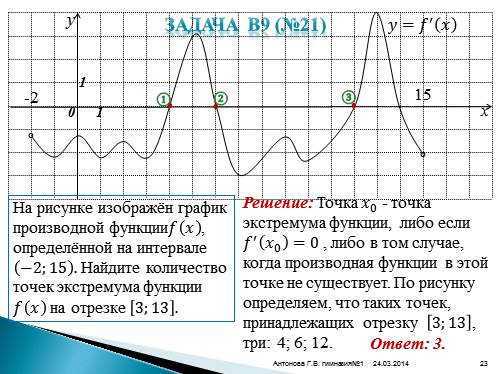
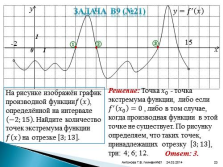
Задача В9 (№21)y
x
0
1
1
-2
15
°
°
????=???? ? ????
На рисунке изображён график производной функции???? ???? , определённой на интервале ?2;15 . Найдите количество точек экстремума функции ???? ???? на отрезке 3;13 . |
Решение: Точка ???? 0 — точка экстремума функции, либо если ???? ? ???? 0 =0 , либо в том случае, когда производная функции в этой точке не существует. По рисунку определяем, что таких точек, принадлежащих отрезку 3;13 , три: 4; 6; 12.
Ответ: 3.
•
•
•
?
?
?Слайд №24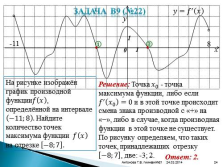 24.03.2016
24.03.2016
Антонова Г.В. гимназия№1
24
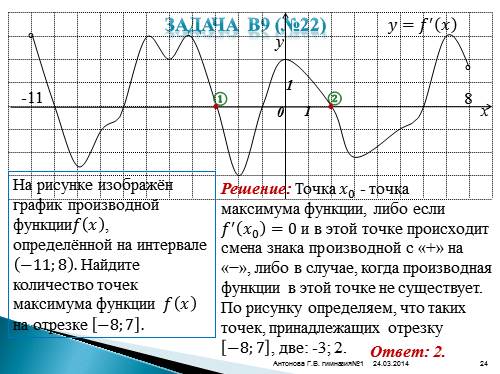
Задача В9 (№22)
y
x
0
1
1
-11
8
°
°
????=???? ? ????
На рисунке изображён график производной функции???? ???? , определённой на интервале ?11;8 . Найдите количество точек максимума функции ???? ???? на отрезке ?8;7 .
Решение: Точка ???? 0 — точка максимума функции, либо если ???? ? ???? 0 =0 и в этой точке происходит смена знака производной с «+» на «?», либо в случае, когда производная функции в этой точке не существует. По рисунку определяем, что таких точек, принадлежащих отрезку ?8;7 , две: -3; 2.
Ответ: 2.
?
?
•
•Слайд №25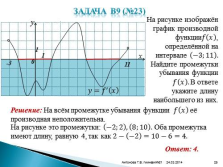 24.03.2016
24.03.2016
Антонова Г.В. гимназия№1
25
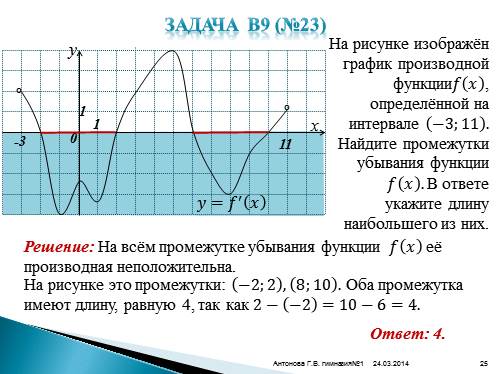
Задача В9 (№23)
????=???? ? ????
°
°
На рисунке изображён график производной функции???? ???? , определённой на интервале ?3;11 . Найдите промежутки убывания функции ???? ???? . В ответе укажите длину наибольшего из них.
-3
11
На рисунке это промежутки: ?2;2 , 8;10 . Оба промежутка имеют длину, равную 4, так как 2? ?2 =10?6=4.
Ответ: 4.
Решение: На всём промежутке убывания функции ???? ???? её производная неположительна.Слайд №26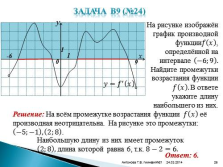 24.03.2016
24.03.2016
Антонова Г.В. гимназия№1
26
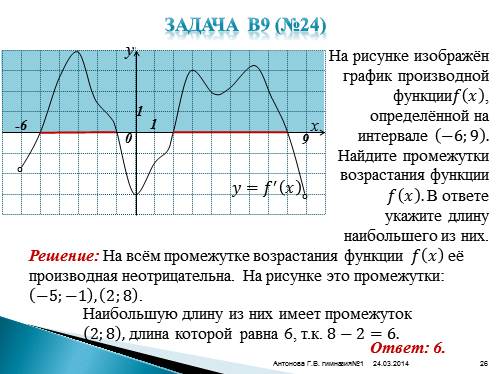
Задача В9 (№24)
На рисунке изображён график производной функции???? ???? , определённой на интервале ?6;9 . Найдите промежутки возрастания функции ???? ???? . В ответе укажите длину наибольшего из них.
-6
9
????=???? ? ????
Решение: На всём промежутке возрастания функции ???? ???? её производная неотрицательна. На рисунке это промежутки: ?5;?1 , 2;8 .
Наибольшую длину из них имеет промежуток 2;8 , длина которой равна 6, т.к. 8?2=6.
Ответ: 6.
°
°Слайд №27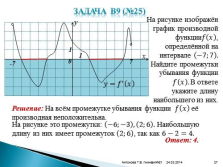 24.03.2016
24.03.2016
Антонова Г.В. гимназия№1
27
Задача В9 (№25)
На рисунке изображён график производной функции???? ???? , определённой на интервале ?7;7 . Найдите промежутки убывания функции ???? ???? . В ответе укажите длину наибольшего из них.
7
-7
°
°
Решение: На всём промежутке убывания функции ???? ???? её производная неположительна.
На рисунке это промежутки: ?6;?3 , 2;6 . Наибольшую
длину из них имеет промежуток 2;6 , так как 6?2=4.
????=???? ? ????
Ответ: 4.Слайд №28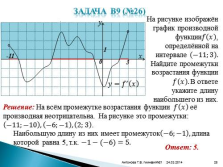 24.03.2016
24.03.2016
Антонова Г.В. гимназия№1
28
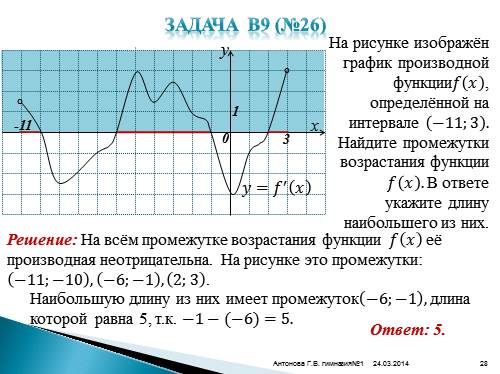
Задача В9 (№26)
На рисунке изображён график производной функции???? ???? , определённой на интервале ?11;3 . Найдите промежутки возрастания функции ???? ???? . В ответе укажите длину наибольшего из них.
-11
3
????=???? ? ????
Решение: На всём промежутке возрастания функции ???? ???? её производная неотрицательна. На рисунке это промежутки: ?11;?10 , ?6;?1 , 2;3 .
Наибольшую длину из них имеет промежуток ?6;?1 , длина которой равна 5, т.к. ?1?(?6)=5.
Ответ: 5.
°
°Слайд №29 24.03.2016
24.03.2016
Антонова Г.В. гимназия№1
29
Задача В9 (№27)
0
х ????
x
•
????=???? ????
????= 1 2 ????+5,5
На рисунке изображен график функции ????=???? ???? и касательная к этому графику, проведённая в точке х ???? . Уравнение касательной показано на рисунке. Найдите значение производной функции ????=4???? ???? +7 в точке х ???? .
Решение: ???? ? (????)= 4???? ???? +7 ? =4? ???? ? ???? ; в точке х ???? значение производной функции равно угловому коэффициенту касательной к графику функции: ???? ? ( ???? 0 )= 1 2 , ?
???? ? ???? 0 =4? ???? ? ???? 0 =4? 1 2 =2.
Ответ: 2.Слайд №30 24.03.2016
24.03.2016
Антонова Г.В. гимназия№1
30
y
0
х ????
х ????
х ????
х ????
х ????
х ????
x
•
•
•
•
•
????=???? ????
Задача В9 (№28)
°
°
•
•
х ????
-5
6
Функция ????=???? ???? определена на интервале ?5;6 . На рисунке изображён график функции ????=???? ???? . Найдите среди точек х ???? , х ???? , х ???? , х ???? , х ???? , х ???? , х ???? те точки, в которых
производная функции равна нулю. В ответ запишите количество найденных точек.
Решение: Производная функции в некоторой точке равна нулю тогда и только тогда, когда касательная к графику функции, проведённая в этой точке, горизонтальна. Этому условию удовлетворяют точки х ???? , х ???? , х ???? и х ???? , ? количество найденных точек равно 4.
Ответ: 4.
Производная в точке х ???? не существуетСлайд №31 24.03.2016
24.03.2016
Антонова Г.В. гимназия№1
31
Задача В9 (№29)
Материальная точка М начинает движение из точки А и движется на протяжении 12 секунд. График показывает, как менялось расстояние от точки М со временем. На оси абсцисс откладывается время t в секундах,
на оси ординат – расстояние s в метрах. Определите, сколько раз за время движения скорость точки М обращалась в ноль (начало и конец движения не учитывайте).
Решение: После начала движения, примерно через 1 с, график достиг верхней точки на этом участке, затем график уходит вниз, ? точка остановилась и стала двигаться назад. Значит каждая вершина и впадина графика означает перемену направления движения точки М, т.е. в этих точках скорость равна 0. Всего на графике 11вершин и впадин, не считая начала и конца движения.
Ответ: 11.Слайд №32
24.03.2016
Антонова Г.В. гимназия№1
Использованная литература
Е33 ЕГЭ 2016. Математика. Типовые тестовые задания /И.Р. Высоцкий, П.И. Захаров и др.; под ред. А.Л.Семёнова, И.В.Ященко. – М.: Издательство «Экзамен», 2014. – 55, ???? с.
Е33 ЕГЭ 2016. Математика. Типовые тестовые задания /И.Р. Высоцкий, П.И. Захаров и др.; под ред. А.Л.Семёнова, И.В.Ященко. – М.: Издательство «Экзамен», 2014. – 95, ???? с.
С30 ЕГЭ: 3000 задач с ответами по математике. Все задания группы В / А.Л.Семёнов, И.В.Ященко, И.Р.Высоцкий и др.; под ред. А.Л.Семёнова, И.В.Ященко. – М.: Издательство «Экзамен»,2014. – 527, ???? с.
32
Оцените статью:
(1 голос, среднее: 5 из 5)
Поделитесь с друзьями!

 24.03.2016
24.03.2016 24.03.2016
24.03.2016 24.03.2016
24.03.2016 24.03.2016
24.03.2016 24.03.2016
24.03.2016 24.03.2016
24.03.2016 24.03.2016
24.03.2016 24.03.2016
24.03.2016