Решение уравнений, содержащих переменную под знаком модуля

Главная Математика

Скачать презентацию (0.75 мб)

Слайды и текст этой презентации

Слайд №1
	Решение уравнений, содержащих переменную под знаком модуля Учитель математики Подгорная Н. П. МБОУ»Скороднянская СОШ»

Слайд №2
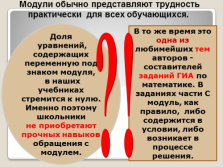	Доля уравнений, содержащих переменную под знаком модуля, в наших учебниках стремится к нулю. Именно поэтому школьники не приобретают прочных навыков обращения с модулем. В то же время это одна из любимейших тем авторов — составителей заданий ГИА по математике. В заданиях части С модуль, как правило, либо содержится в условии, либо возникает в процессе решения. Модули обычно представляют трудность практически для всех обучающихся. ?!
Слайд №3
	Поэтому, задача учителя помочь обучающимся научиться обращаться с такими заданиями правильно, вооружить их различными приёмами и способами решения уравнений с модулем.
Слайд №4
	Мало кто из учащихся к 11 классу помнит о смысле понятия «модуль». Если же найдутся те, кто помнит формально – описательную структуру для раскрытия модуля то скорее всего дальше этой записи дело не пойдёт, так как учащиеся совершенно не могут её применять при решении уравнений.
Слайд №5
	Поэтому в первую очередь на самых простых примерахвосстанавливаем представление о понятии «модуль». Правило из трёх словдолжен запомнить каждый. А затем уточняем, расстояние между чем и чем. МОДУЛЬ — ЭТО РАССТОЯНИЕ
Слайд №6
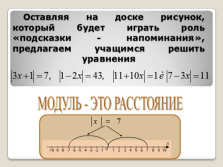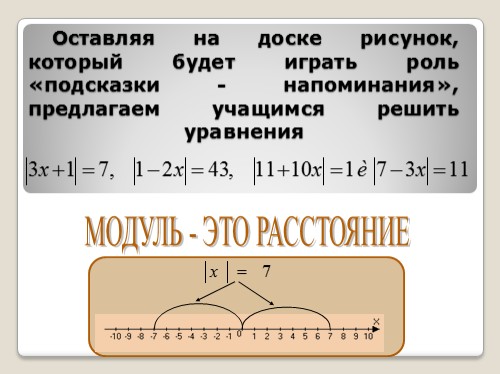
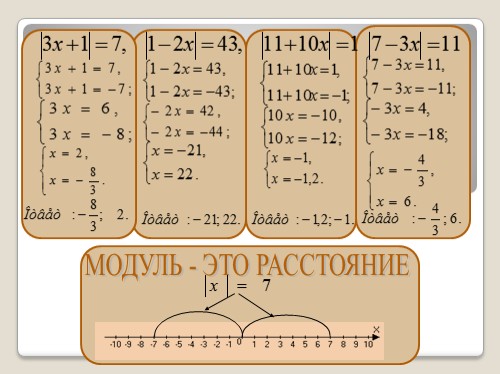
	Оставляя на доске рисунок, который будет играть роль «подсказки — напоминания», предлагаем учащимся решить уравнения МОДУЛЬ — ЭТО РАССТОЯНИЕ
Слайд №7
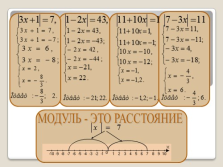	МОДУЛЬ — ЭТО РАССТОЯНИЕ
Слайд №8
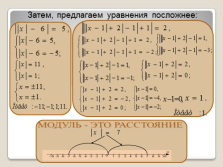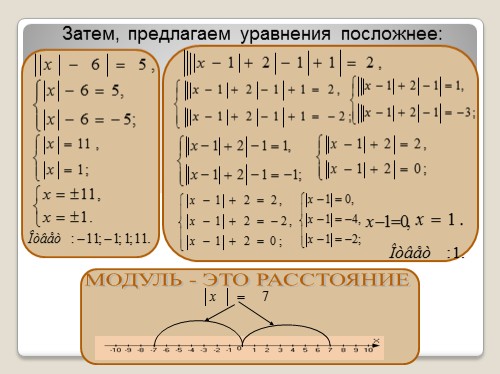
	МОДУЛЬ — ЭТО РАССТОЯНИЕ Затем, предлагаем уравнения посложнее:
Слайд №9
	Следующий шаг в освоении этой темы – решение уравнений, содержащих несколько выражений, стоящих под знаками модуля. Для их решения воспользуемся методом последовательного раскрытия модулей. Находим точки в которых каждое выражение, стоящее под знаком модуля, может менять свой знак. Отмечаем найденные точки на числовой оси. (Мы получили интервалы знакопостоянства выражений, стоящих под знаками модуля.) На каждом интервале модули выражений раскрываем в соответствии с их знаками.
Слайд №10
	Решим уравнения: — + + — 0 — 2 + — -2 — 3 + — + +
Слайд №11
	Следующий шаг — решение уравнений вида . Из определения и свойств модуля непосредственно следует, Поэтому,
Слайд №12
	Но чаще бывает выгодно использовать область значений функции и записать другую систему, равносильную этому уравнению:
Слайд №13
	Решим уравнения:
Слайд №14
	Уважаемые коллеги, спасибо за внимание! Надеюсь, этот материал будет вам полезен!