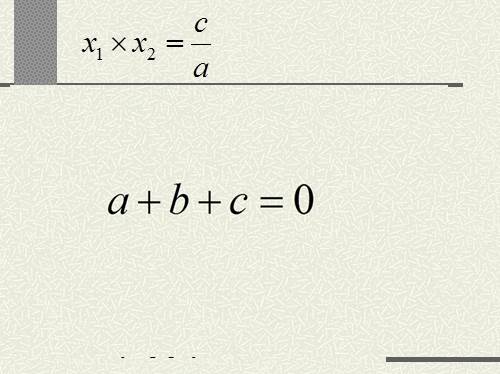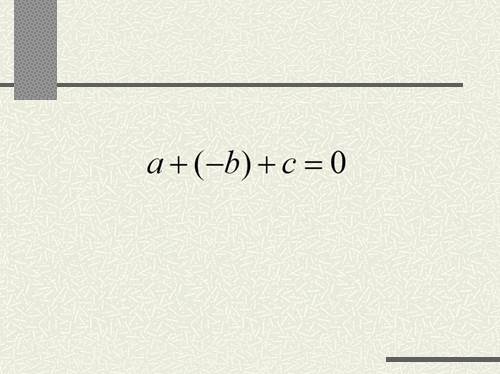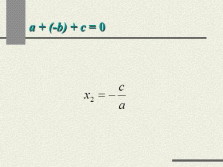Формулы Виета и устное решение квадратных уравнений

Главная Алгебра

Скачать презентацию (1.15 мб)

Слайды и текст этой презентации

Слайд №1
	Формулы Виета и устное решение квадратных уравнений Кузнецова Лариса Викторовна учитель математики МБОУ СОШ №1 г. Климовск

Слайд №2
	Теорема Виета Если x1 и x2 – корни квадратного уравнения , то:
Слайд №3
	Найти корни уравнений
Слайд №4
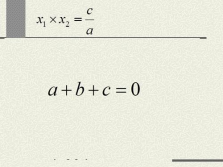	Будет ли число 1 – корнем уравнений сделайте вывод о соотношении коэффициентов этих уравнений, найдите другой корень уравнения, используя формулы Виета
Слайд №5
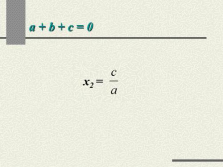	a + b + c = 0
Слайд №6
	a + b + c = 0 Если квадратное уравнение имеет корни и тогда
Слайд №7
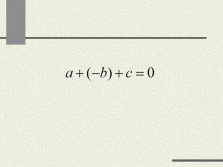	Будет ли число -1 – корнем уравнений сделайте вывод о соотношении коэффициентов этих уравнений; найдите второй корень уравнения, используя формулы Виета.
Слайд №8
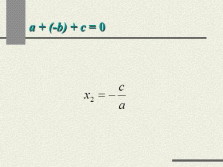	а + (-b) + c = 0
Слайд №9
	a + (-b) + c = 0 Если квадратное уравнение имеет корни и тогда
Слайд №10
	Найти корни уравнений
Слайд №11
	Решение уравнений 1) 2)
Слайд №12
	Решаем сами Найти корни уравнения: Решение: Ответ:
Слайд №13
	Решаем сами По учебному пособию М.П. Галицкого и др. № 5.75(а,б); 5.76(а,б); 5.77(а,б); 5.78(а,б).
Слайд №14
	Домашнее задание По учебному пособию М.П. Галицкого и др. № 5.75(в, г); 5.76(в, г); 5.77(в, г); 5.78(в ,г). Придумать квадратные уравнения, с большими коэффициентами, решаемые устно. Для сильных учащихся — доказательство утверждений, используемых на уроке.
Слайд №15
	Список ресурсов: 1) Ю.Н. Миндюк, Н.Г. Миндюк. Алгебра. Дополнительные главы к школьному учебнику 8 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики. Под редакцией Г.В. Дорофеева. М. «Просвещение» 1996. 2) М.Л. Галицкий, А.М Гольдман, Л.И. Звавич. Сборник задач по алгебре для 8 – 9 классов. Учебное пособие для учащихся школ и классов с углубленным изучением математики. М. «Просвещение» 1992.
Слайд №16
	Список ресурсов: 5) портрет Виета http://www.mathresources.com/products/mathresource/dictionary/thumbs/viete.png