Методы решения систем уравнений

Главная Алгебра

Скачать презентацию (1.75 мб)

Слайды и текст этой презентации

Слайд №1
	МОУ — СОШ №6 Учитель математики Миссюра Ирина Николаевна Методы решения систем уравнений

Слайд №2
	Цель урока Продолжить формирование навыков сознательного выбора способа решения системы; Развивать потребность в нахождении рациональных способов решения; Воспитывать умение контролировать внимание на всех этапах урока;
Слайд №3
	«Математику нельзя изучать, наблюдая как это делает сосед»
Слайд №4
	ТЕСТпо теме «Подготовка к ГИА » 7 – 9 классы
Слайд №5
	1. Вычислите: Проверка
Слайд №6
	2. Упростите выражение Проверка
Слайд №7
	3. Разложите на множители Проверка
Слайд №8
	4. Выполните умножение Проверка
Слайд №9
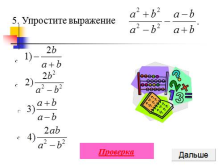	5. Упростите выражение Проверка
Слайд №10
	6. Сколько процентов составляет число 8 от своего квадрата? Проверка
Слайд №11
	7. Найдите наибольший корень уравнения Проверка
Слайд №12
	8. Решите неравенство Проверка
Слайд №13
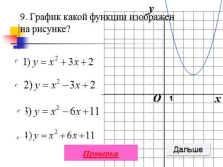	9. График какой функции изображен на рисунке? O x 1 y Проверка
Слайд №14
	Б. В. 1 Г. При х = — 4/9 выражение не имеет смысла. А. 10. Найдите значение выражения Проверка
Слайд №15
	A. A = Nt В. Г. Б. 11. Из формулы мощности N=A/t выразите работу A. Проверка
Слайд №16
	А. В. Г. Б. 12. Упростите выражение Проверка
Слайд №17
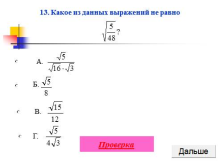	13. Какое из данных выражений не равно А. Б. В. Г. Проверка
Слайд №18
	14. Велосипедист от озера до деревни ехал со скоростью 15км/ч, а обратно – со скоростью 10 км/ч. Сколько времени ушло у него на дорогу от озера до деревни, если на весь путь туда и обратно велосипедист затратил 1 ч? Пусть х ч – время, затраченное на дорогу от озера до деревни. Какое из уравнений соответствует условию задачи? А. Б. 15х = 10(1 – х) В. 15х + 10(1 – х) = 1 Г. 15(1 – х) = 10х Проверка
Слайд №19
	Ответ: 2. РЕШЕНИЕ:
Слайд №20
	Ответ: 2. 2. Упростите выражение РЕШЕНИЕ:
Слайд №21
	Ответ: 2. 3. Разложите на множители РЕШЕНИЕ:
Слайд №22
	Ответ: 1. 4. Выполните умножение РЕШЕНИЕ:
Слайд №23
	РЕШЕНИЕ: Ответ: 4.
Слайд №24
	6. Сколько процентов составляет число 8 от своего квадрата? Решение: % Ответ: 3.
Слайд №25
	7. Найдите наибольший корень уравнения РЕШЕНИЕ: a + b + c = 2 + 3 – 5 = 0, значит х1 = 1, х2 = — 5 : 2 = — 2,5. Наибольший корень уравнения х = 1. Ответ: 1.
Слайд №26
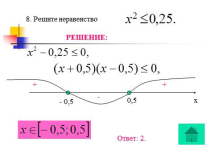	8. Решите неравенство РЕШЕНИЕ: х — 0,5 0,5 + + — Ответ: 2.
Слайд №27
	9. График какой функции изображен на рисунке? РЕШЕНИЕ: Ответ: 3.
Слайд №28
	10. Найдите значение выражения РЕШЕНИЕ: Ответ: Б.
Слайд №29
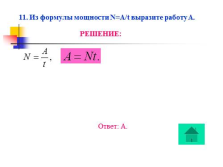	11. Из формулы мощности N=A/t выразите работу A. РЕШЕНИЕ: Ответ: А.
Слайд №30
	13. Упростите выражение РЕШЕНИЕ: Ответ: А.
Слайд №31
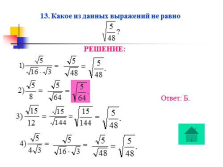	13. Какое из данных выражений не равно РЕШЕНИЕ: Ответ: Б.
Слайд №32
	14. Велосипедист от озера до деревни ехал со скоростью 15км/ч, а обратно – со скоростью 10 км/ч. Сколько времени ушло у него на дорогу от озера до деревни, если на весь путь туда и обратно велосипедист затратил 1 ч? Пусть х ч – время, затраченное на дорогу от озера до деревни. Какое из уравнений соответствует условию задачи? РЕШЕНИЕ: Если х ч – время затраченное на дорогу от озера до деревни и все время 1 ч, то на путь обратно велосипедист затратил (1 – х) ч. 15х км – расстояние от озера до деревни, 10(1 – х) км – расстояние от деревни до озера. Зная, что расстояния одинаковые, составляем уравнение: Ответ: Б.
Слайд №33
	Алгебра стоит на четырёх китах Число Тождество Функция Алгебра щедра. Зачастую она дает больше, чем у нее спрашивают Ж.Даламбер число уравнение тождество функция
Слайд №34
	Определение Уравнение – это равенство, содержащее одну или несколько переменных Линейное уравнение с одной переменной Линейное уравнение с двумя переменными Свойства уравнений если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному Уравнение и его свойства
Слайд №35
	Вопросы для размышления Являются ли данные выражения уравнениями? a) 5x + 4 = 0; b) 2 + 3x; c) 7x + 3 = 4y; d) 7x + 5y; Равносильны ли эти уравнения? 2x + 3y = 10 и 2x = 10 – 3y; 10 – 2x = 5y и 10 = 5y – 2x; Равносильны ли эти уравнения? 2x + y = 3 и 4x +2y = 6; 21x + 15 = 3y и 7x + 5 = 9y; Выпишите буквы правильных ответов
Слайд №36
	Что называется системой уравнений? Что называется решением системы уравнений? Что значит – решить систему уравнений?
Слайд №37
	Система уравнений и её решение Определения Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство Решить систему уравнений — это значит найти все её решения или установить, что их нет
Слайд №38
	Сколько решений имеет система уравнений ? Если к1 к2 Графики пересекаются Система имеет единственное решение Если к1=к2, b1 b2 Графики параллельны Система не имеет решений Если к1=к2, b1=b2 Графики совпадают Система имеет бесконечно много решений
Слайд №39
	Является ли пара чисел решением системы (3;1) (2;2) верно неверно верно верно (3;1) не является решением (2;2) является решением
Слайд №40
	Методы решения систем уравнений способ подстановки способ сложения графический способ
Слайд №41
	Решить систему уравнений способом подстановки y – 2x = 4 , 7x – y = 1 .
Слайд №42
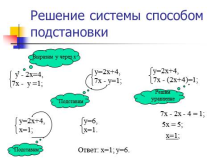	Решение системы способом подстановки 7х — 2х — 4 = 1; 5х = 5; х=1; Ответ: х=1; у=6.
Слайд №43
	Способ подстановки (алгоритм) Из какого-либо уравнения выразить одну переменную через другую Подставить полученное выражение для переменной в другое уравнение и решить его Сделать подстановку найденного значения переменной и вычислить значение второй переменной Записать ответ: х=…; у=… .
Слайд №44
	Решить систему уравнений способом сложения 7x + 2y = 1 , 17x + 6y = -9 .
Слайд №45
	Решение системы способом сложения \|\|·(-3) + ____________ Ответ: (3; — 10)
Слайд №46
	Способ сложения (алгоритм) Уравнять модули коэффициентов при какой-нибудь переменной Сложить почленно уравнения системы Составить новую систему: одно уравнение новое, другое — одно из старых Решить новое уравнение и найти значение одной переменной Подставить значение найденной переменной в старое уравнение и найти значение другой переменной Записать ответ: х=…; у=… .
Слайд №47
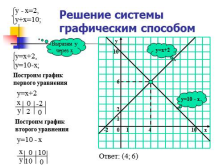	Решение системы графическим способом y=10 — x y=x+2 Выразим у через х Построим график первого уравнения у=х+2 Построим график второго уравнения у=10 — х Ответ: (4; 6)
Слайд №48
	Графический способ (алгоритм) Выразить у через х в каждом уравнении Построить в одной системе координат график каждого уравнения Определить координаты точки пересечения Записать ответ: х=…; у=… , или (х; у)
Слайд №49
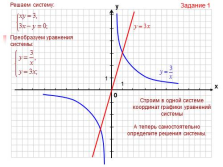	Задание 1 Строим в одной системе координат графики уравнений системы А теперь самостоятельно определите решения системы.
Слайд №50
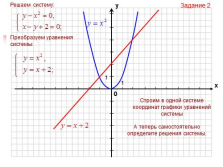	Задание 2 Строим в одной системе координат графики уравнений системы А теперь самостоятельно определите решения системы.
Слайд №51
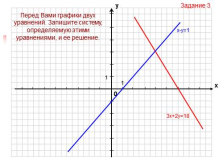	Задание 3 3х+2у=18 Перед Вами графики двух уравнений. Запишите систему, определяемую этими уравнениями, и ее решение.
Слайд №52
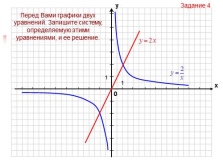	Перед Вами графики двух уравнений. Запишите систему, определяемую этими уравнениями, и ее решение. Задание 4
Слайд №53
	Применение систем уравнений 1. В настоящее время в компьютерной технологии широко используются электронные таблицы для решения задач управления в промышленности, бизнесе, финансовой деятельности. Электронная таблица легко позволяет реализовать один из методов вычислительной математики — метод итераций. Наибольшее применение итерационный метод нашел при решении систем линейных уравнений. К таким системам сводятся задачи анализа электрических цепей, расчета энергий колебательных уровней двухатомных молекул и др. Метод используется и для решения систем нелинейных уравнений: система «хищник-жертва» и др. 2. Решение задачи о месте и времени встречи промыслового рыболовецкого судна с перегрузчиком сводится по сути к решению систем линейных уравнений, использующих данные о координатах судов, их скоростях и метеоусловиях.
Слайд №54
	Самостоятельная работа Решите системы уравнений
Слайд №55
	Домашнее задание: п.6 (определение, примеры) № 6.7(а,б) № 6.8(а,б)сборник ГИА №3.5
Слайд №56
	Спасибо всем за работу
Слайд №57
	ИСПОЛЬЗОВАННЫЕ РЕСУРСЫ: ШАБЛОН – СЕТЬ ТВОРЧЕСКИХ УЧИТЕЛЕЙ «СОЗДАНИЕ ИНТЕРАКТИВНЫХ ТЕСТОВ НА УРОКАХ МАТЕМАТИКИ» Савченко Е. М. КАРТИНКИ – КОЛЛЕКЦИЯ ОБРАЗОВАТЕЛЬНЫХ РЕСУРСОВ И СЕТЬ ТВОРЧЕСКИХ УЧИТЕЛЕЙ «АЛГЕБРА» Сборник заданий для подготовки к итоговой аттестации в 9 классе. Москва. Просвещение. 2011.