Построение сечений многогранников
Скачать презентацию (2.28 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Тема: « Задачи на построение сечений». Автор работы: Янаева Ольга Николаевна, учитель математики МБУ гимназии №35 г.о. Тольятти |
| Слайд №2 | |
 |
Цели урока Знать алгоритм решения задач методом «следов» и методом параллельного проецирования; Уметь решать задачи на построение сечений; Уметь применять алгоритм при решении задач на построение сечений; |
| Слайд №3 | |
 |
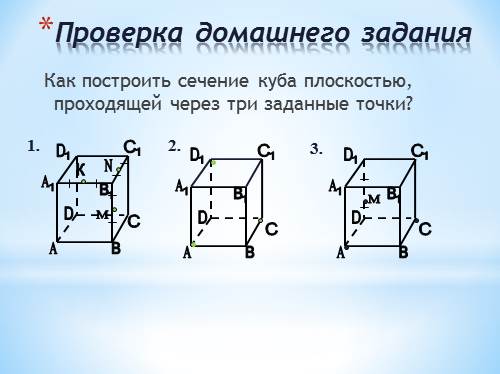
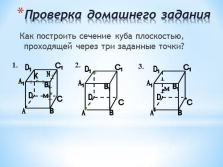
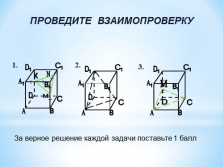
А А 1 в в 1 D D 1 С С 1 А А 1 в в 1 D D 1 С С 1 А А 1 в в 1 D D 1 С С 1 Проверка домашнего задания Как построить сечение куба плоскостью, проходящей через три заданные точки? 1. 2. 3. к N M M |
| Слайд №4 | |
 |
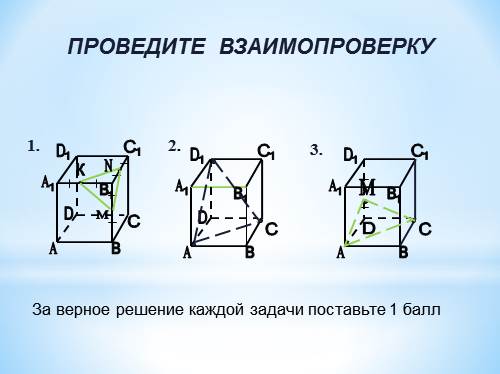
А А 1 в в 1 D D 1 С С 1 А А 1 в в 1 D D 1 С С 1 А А 1 в в 1 D D 1 С С 1 к N M M 1. 2. 3. ПРОВЕДИТЕ ВЗАИМОПРОВЕРКУ За верное решение каждой задачи поставьте 1 балл |
| Слайд №5 | |
 |
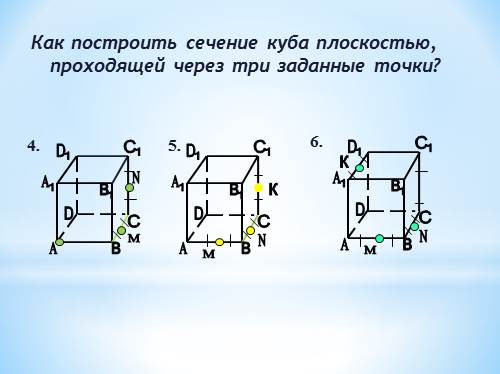
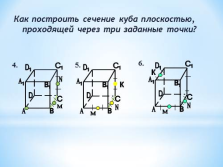
А А 1 в в 1 D D 1 С С 1 4. N M А А 1 в в 1 D D 1 С С 1 N M к А А 1 в в 1 D D 1 С С 1 N M к 5. 6. Как построить сечение куба плоскостью, проходящей через три заданные точки? |
| Слайд №6 | |
 |
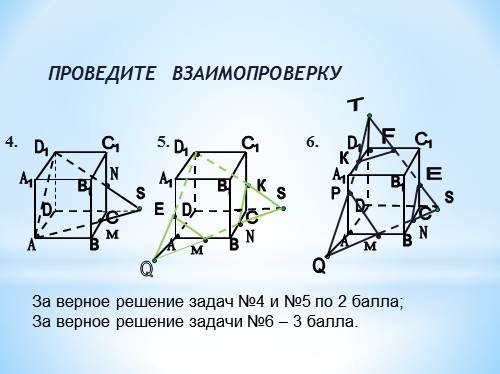
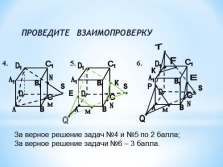
А А 1 в в 1 D D 1 С С 1 4. N M А А 1 в в 1 D D 1 С С 1 N M к 5. E Q А А 1 в в 1 D D 1 С С 1 N M к P Q E F 6. s s s T ПРОВЕДИТЕ ВЗАИМОПРОВЕРКУ За верное решение задач №4 и №5 по 2 балла; За верное решение задачи №6 – 3 балла. |
| Слайд №7 | |
 |
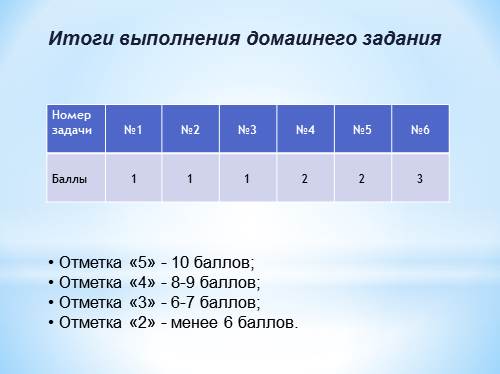
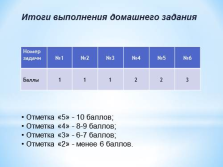
Номер задачи №1 №2 №3 №4 №5 №6 Баллы 1 1 1 2 2 3 Отметка «5» — 10 баллов; Отметка «4» — 8-9 баллов; Отметка «3» — 6-7 баллов; Отметка «2» — менее 6 баллов. Итоги выполнения домашнего задания |
| Слайд №8 | |
 |
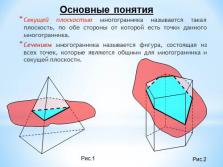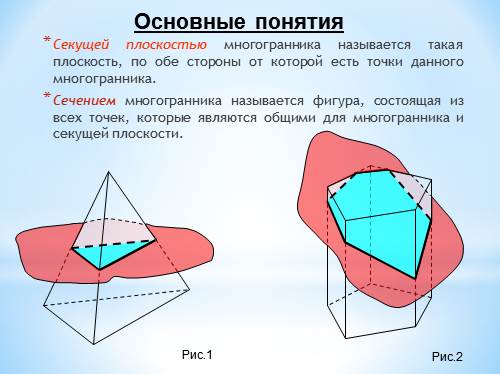
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть точки данного многогранника. Сечением многогранника называется фигура, состоящая из всех точек, которые являются общими для многогранника и секущей плоскости. Основные понятия Рис.1 Рис.2 |
| Слайд №9 | |
 |
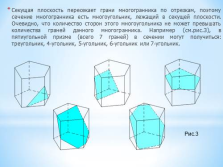Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон этого многоугольника не может превышать количества граней данного многогранника. Например (см.рис.3), в пятиугольной призме (всего 7 граней) в сечении могут получиться: треугольник, 4-угольник, 5-угольник, 6-угольник или 7-угольник. Рис.3 |
| Слайд №10 | |
 |
Две плоскости пересекаются по прямой (эта аксиома и дала названию метода – под «следом» понимается прямая пересечения какой-либо грани многогранника и секущей плоскости). Получение «следа» сводится к получению двух точек, принадлежащих одновременно какой-нибудь грани многогранника и секущей плоскости (подумайте, почему именно двух!?). Точки получаются как пересечение двух прямых, принадлежащих одной и той же плоскости. ПРИМЕЧАНИЕ. Не забудьте, что прямая и плоскость являются бесконечными в пространстве фигурами! Проследим на примере построение сечения куба плоскостью, заданной тремя данными точками M, N и K. |
| Слайд №11 | |
 |
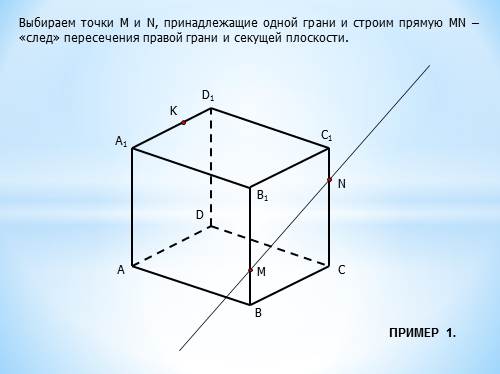
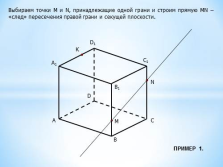
A B C D B1 C1 D1 M N K Выбираем точки М и N, принадлежащие одной грани и строим прямую MN – «след» пересечения правой грани и секущей плоскости. A1 ПРИМЕР 1. |
| Слайд №12 | |
 |
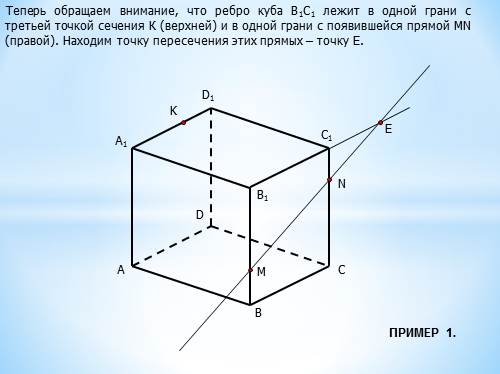
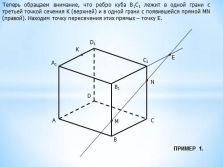
A B C D B1 C1 D1 M N K A1 E Теперь обращаем внимание, что ребро куба В1С1 лежит в одной грани с третьей точкой сечения К (верхней) и в одной грани с появившейся прямой MN (правой). Находим точку пересечения этих прямых – точку Е. ПРИМЕР 1. |
| Слайд №13 | |
 |
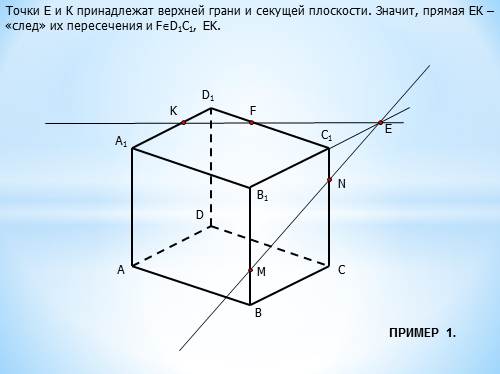
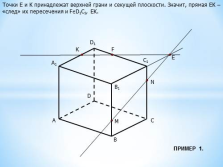
A B C D B1 C1 D1 M N K A1 E Точки Е и К принадлежат верхней грани и секущей плоскости. Значит, прямая ЕК – «след» их пересечения и F?D1C1, EK. F ПРИМЕР 1. |
| Слайд №14 | |
 |
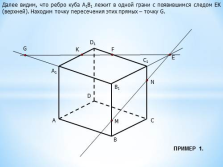
A B C D B1 C1 D1 M N K A1 E F Далее видим, что ребро куба А1В1 лежит в одной грани с появившимся следом ЕК (верхней). Находим точку пересечения этих прямых – точку G. G ПРИМЕР 1. |
| Слайд №15 | |
 |
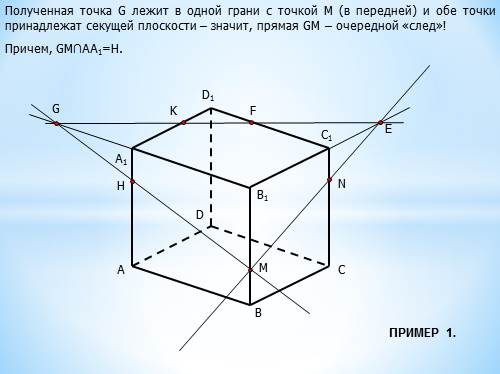
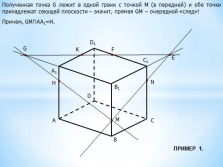
A B C D B1 C1 D1 M N K A1 E F G Полученная точка G лежит в одной грани с точкой М (в передней) и обе точки принадлежат секущей плоскости – значит, прямая GM – очередной «след»! Причем, GM?АА1=Н. H ПРИМЕР 1. |
| Слайд №16 | |
 |
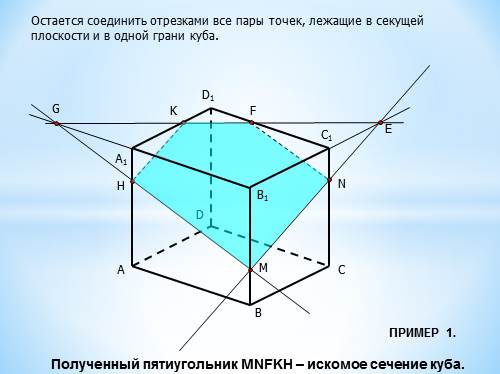
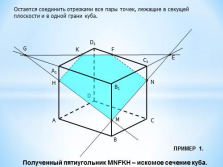
A B C D C1 D1 M N K A1 E F G H Остается соединить отрезками все пары точек, лежащие в секущей плоскости и в одной грани куба. Полученный пятиугольник MNFKH – искомое сечение куба. B1 ПРИМЕР 1. |
| Слайд №17 | |
 |
Плоскость сечения может задаваться: 1) тремя точками, не лежащими на одной прямой; 2) прямой и точкой, не лежащей на ней; 3) двумя пересекающимися прямыми; 4) двумя параллельными прямыми. Все эти случаи можно свести к первому, выбирая на прямых удобные для нас точки. |
| Слайд №18 | |
 |
Данный метод построения сечений многогранников можно применять, если найдется хотя бы одна пара точек, лежащих в секущей плоскости и одной грани многогранника. После чего задача циклично алгоритмизируется в получение очередной точки и очередного «следа». ПРИМЕЧАНИЕ. Если такой пары точек не найдется, то сечение строится методом параллельных проекций. |
| Слайд №19 | |
 |
Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны. |
| Слайд №20 | |
 |
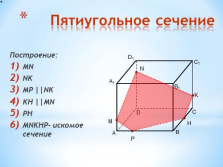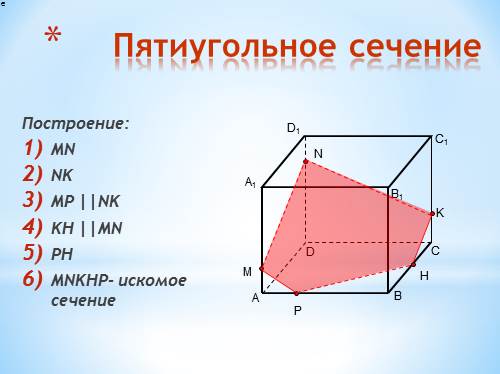
Пятиугольное сечение Построение: MN NK MP ||NK KH ||MN PH MNKHP- искомое сечение A |
| Слайд №21 | |
 |
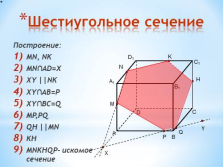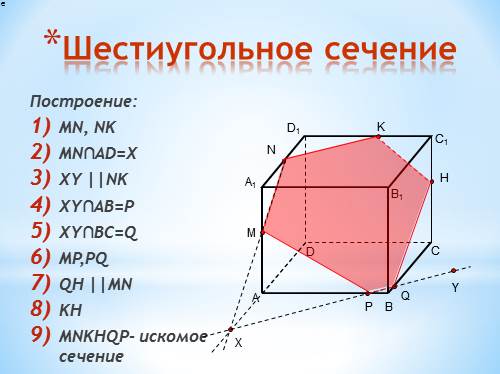
Шестиугольное сечение Построение: MN, NK MN?AD=X XY ||NK XY?AB=P XY?BC=Q MP,PQ QH ||MN KH MNKHQP- искомое сечение A |
| Слайд №22 | |
 |
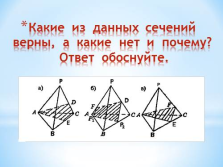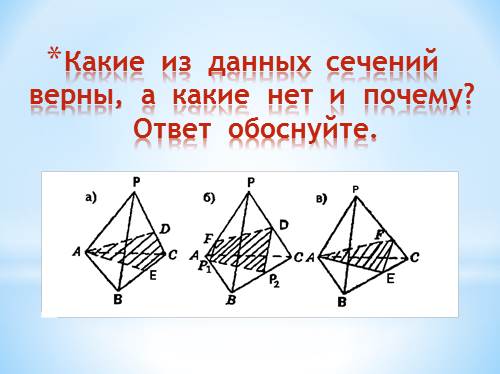
Какие из данных сечений верны, а какие нет и почему? Ответ обоснуйте. |
| Слайд №23 | |
 |
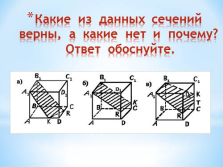Какие из данных сечений верны, а какие нет и почему? Ответ обоснуйте. |
| Слайд №24 | |
 |
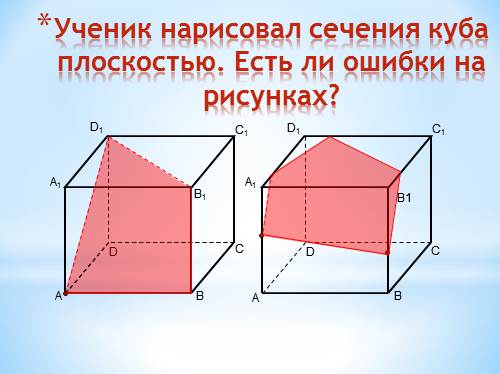
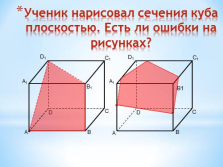
A B D C A1 C1 D1 A B C D A1 D1 C1 B1 B1 Ученик нарисовал сечения куба плоскостью. Есть ли ошибки на рисунках? |
| Слайд №25 | |
 |
Спасибо за урок! |
