Смежные и вертикальные углы
Скачать презентацию (0.14 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Начальные геометрические сведения 7 классгеометрия Урок №7 Смежные и вертикальные углы 13.07.2012 1 www.konspekturoka.ru |
| Слайд №2 | |
 |
Цели: 13.07.2012 Ознакомить с понятием смежных и вертикальных углов, рассмотреть их свойства; Научить строить угол, смежный с данным углом, изображать вертикальные углы, находить на рисунке вертикальные и смежные углы. 2 www.konspekturoka.ru |
| Слайд №3 | |
 |
13.07.2012 www.konspekturoka.ru 3 Луч ОС делит < АОВ на два <АОС , <СОВ – смежные углы Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Изучение нового материала |
| Слайд №4 | |
 |
13.07.2012 www.konspekturoka.ru 4 3 угла: < АОВ — развернутый <АОС , <СОВ – смежные углы Сколько углов изображено на рисунке? Изучение нового материала |
| Слайд №5 | |
 |
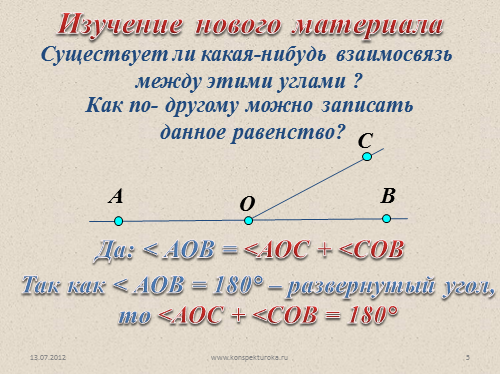
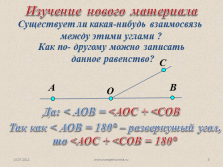
13.07.2012 www.konspekturoka.ru 5 Да: < АОВ = <АОС + <СОВ Существует ли какая-нибудь взаимосвязь между этими углами ? Изучение нового материала Как по- другому можно записать данное равенство? Так как < АОВ = 180° – развернутый угол, то <АОС + <СОВ = 180° |
| Слайд №6 | |
 |
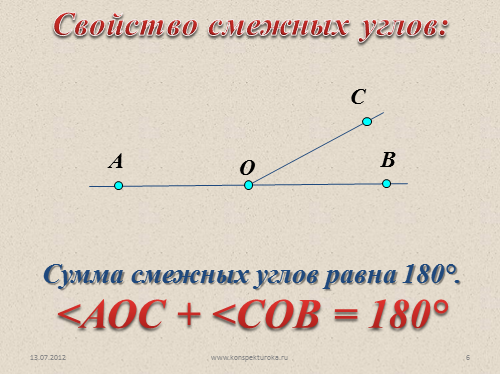
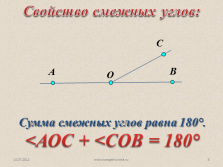
13.07.2012 www.konspekturoka.ru 6 Свойство смежных углов: Сумма смежных углов равна 180°. <АОС + <СОВ = 180° |
| Слайд №7 | |
 |
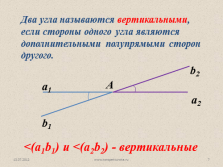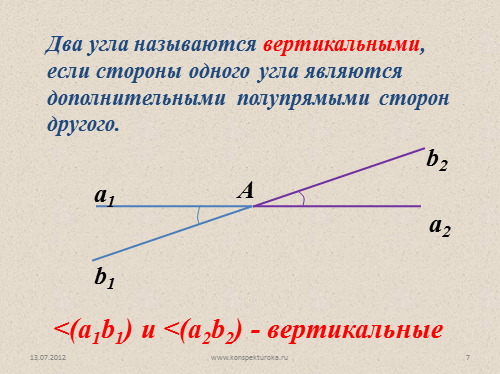
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. а1 а2 b1 b2 A <(а1b1) и <(a2b2) — вертикальные 13.07.2012 7 www.konspekturoka.ru |
| Слайд №8 | |
 |
Построение вертикальных углов S F 13.07.2012 8 www.konspekturoka.ru |
| Слайд №9 | |
 |
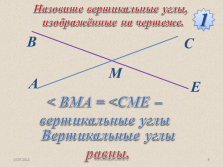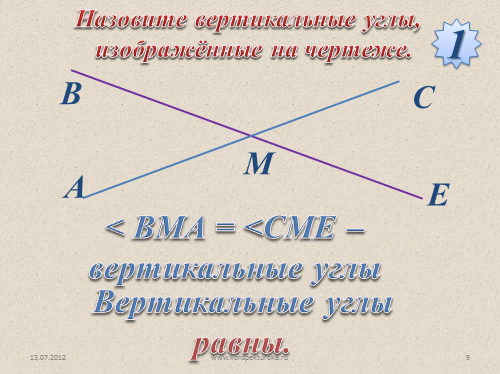
Назовите вертикальные углы, изображённые на чертеже. 1 < BMA = <CME – вертикальные углы Вертикальные углы равны. 13.07.2012 9 www.konspekturoka.ru |
| Слайд №10 | |
 |
13.07.2012 www.konspekturoka.ru 10 Назовите вертикальные углы, изображённые на чертеже. 2 1 2 3 4 5 6 7 8 9 10 11 12 <1 и <2; <11 и <12; <3 и <10; <9 и <8; <4 и <6; <5 и <7. |
| Слайд №11 | |
 |
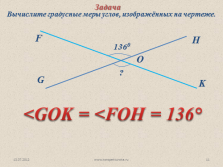
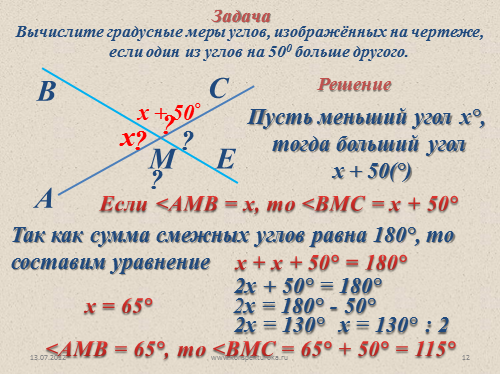
13.07.2012 www.konspekturoka.ru 11 G F O H K 1360 ? Задача Вычислите градусные меры углов, изображённых на чертеже. <GOK = <FOH = 136° |
| Слайд №12 | |
 |
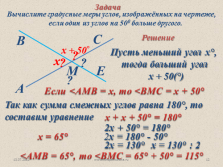
A В М С Е ? ? ? ? Вычислите градусные меры углов, изображённых на чертеже, если один из углов на 500 больше другого. Задача Решение Пусть меньший угол х°, тогда больший угол х + 50(°) х х + 50° Если <АМВ = х, то <ВМС = х + 50° Так как сумма смежных углов равна 180°, то составим уравнение х + х + 50° = 180° 2х + 50° = 180° 2х = 180° — 50° 2х = 130° х = 130° : 2 х = 65° <АМВ = 65°, то <ВМС = 65° + 50° = 115° 13.07.2012 12 www.konspekturoka.ru |
| Слайд №13 | |
 |
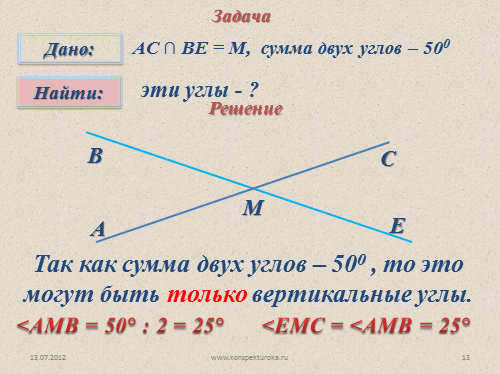
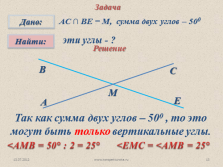
13.07.2012 www.konspekturoka.ru 13 Задача эти углы — ? АС ? ВЕ = М, сумма двух углов – 500 Решение Так как сумма двух углов – 500 , то это могут быть только вертикальные углы. <АМВ = 50° : 2 = 25° <ЕМС = <АМВ = 25° |
| Слайд №14 | |
 |
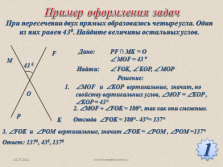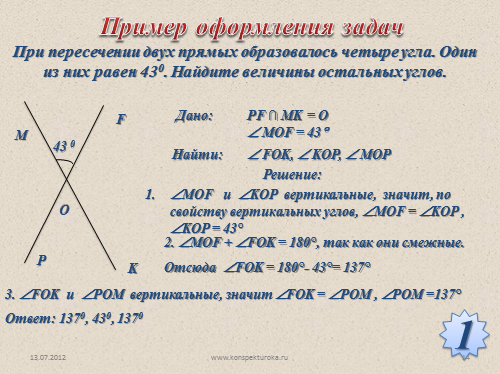
Пример оформления задач При пересечении двух прямых образовалось четыре угла. Один из них равен 430. Найдите величины остальных углов. Дано: PF ? MK = O ? MOF = 43? Найти: ? FOK, ? KOP, ? MOP Решение: ?МОF и ?KOP вертикальные, значит, по свойству вертикальных углов, ?МОF = ?KOP , ?KOP = 43° 2. ?МОF + ?FOK = 180°, так как они смежные. Отсюда ?FOK = 180°- 43°= 137° 3. ?FOK и ?POM вертикальные, значит ?FOK = ?POM , ?POM =137° Ответ: 1370, 430, 1370 1 13.07.2012 14 www.konspekturoka.ru |
| Слайд №15 | |
 |
Один из смежных углов на 320 больше другого. Найдите величину каждого угла. Дано: ?АОВ и ?ВОС смежные, ?АОВ — ?ВOС = 32°. Найти: ?АOВ , ?ВOС . Решение: Пусть ? ВОС = х, тогда ? АОВ = 32+х По свойству смежных углов составим уравнение x + (32?+x) = 180? 2x = 180? — 32? 2x = 148? x= 74? Значит ? ВОС = 74?, а ? АОВ = 32?+74?=106? Ответ: ? АОВ = 106?, ? ВОС = 74? Пример оформления задач 2 13.07.2012 15 www.konspekturoka.ru |
| Слайд №16 | |
 |
13.07.2012 16 Ответить на вопросы: Какие углы называем смежными? Какие углы называем вертикальными? Назвать свойство смежных углов. Как построить смежные углы? Назвать свойство вертикальных углов. Как построить вертикальные углы? www.konspekturoka.ru |
