Сравнение и измерение углов
Скачать презентацию (0.21 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Начальные геометрические сведения 7 классгеометрия Уроки №5-6 Сравнение и измерение углов 13.07.2012 1 www.konspekturoka.ru |
| Слайд №2 | |
 |
Цели: 13.07.2012 Ввести понятие равенства геометрических фигур. Научить сравнивать углы. Ввести понятие биссектрисы угла, научить строить используя транспортир. Ввести понятие градуса и градусной меры угла. Рассмотреть свойства градусных мер угла, свойство измерения углов. Повторить виды углов. 2 www.konspekturoka.ru |
| Слайд №3 | |
 |
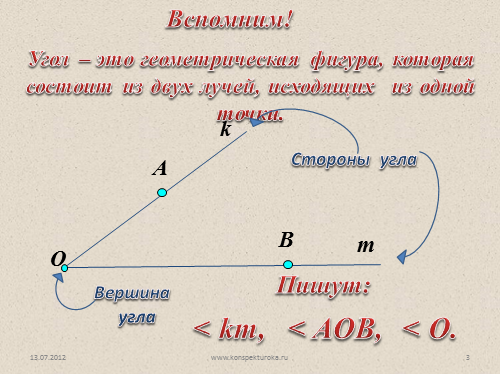
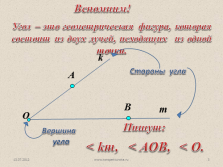
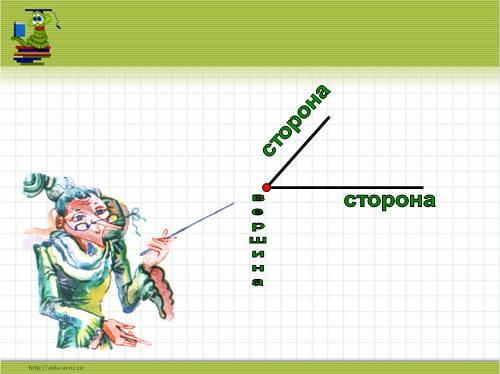
13.07.2012 www.konspekturoka.ru 3 k Угол – это геометрическая фигура, которая состоит из двух лучей, исходящих из одной точки. O Вспомним! |
| Слайд №4 | |
 |
Угол – называется развернутым, если его обе стороны лежат на одной прямой (каждая сторона развернутого угла является продолжением другой стороны). развернутый угол < hm, < A Вспомним! 13.07.2012 4 www.konspekturoka.ru |
| Слайд №5 | |
 |
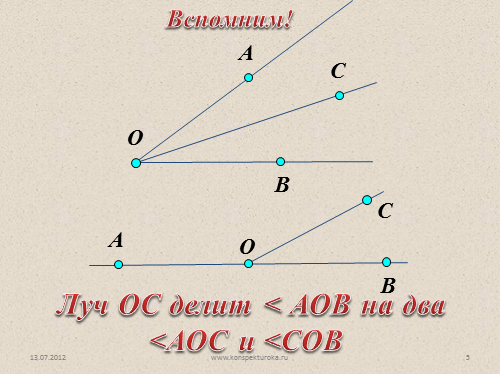
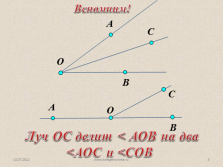
13.07.2012 www.konspekturoka.ru 5 Луч ОС делит < АОВ на два <АОС и <СОВ Вспомним! |
| Слайд №6 | |
 |
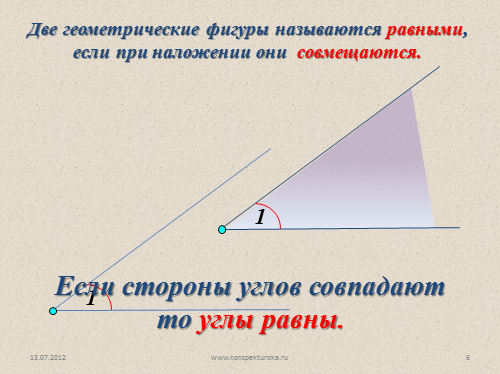
13.07.2012 www.konspekturoka.ru 6 1 Две геометрические фигуры называются равными, если при наложении они совмещаются. Если стороны углов совпадают то углы равны. |
| Слайд №7 | |
 |
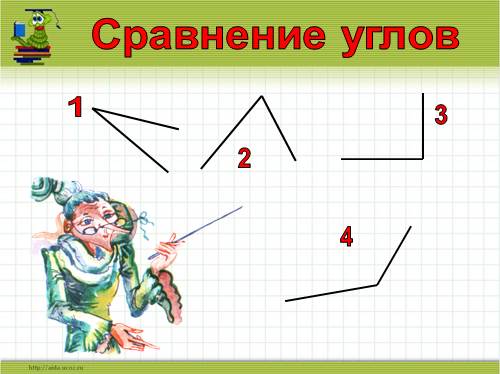
13.07.2012 www.konspekturoka.ru 7 1 Если стороны углов не совместятся, то меньшим считается тот угол, который составляет часть другого. Стороны углов не совпадают, то углы не равны. Угол 2 меньше угла 1 Пишут: <2 < <1 |
| Слайд №8 | |
 |
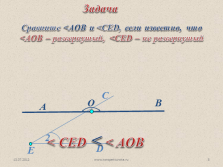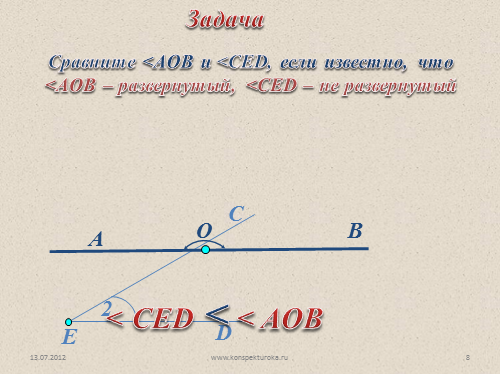
Сравните <AOB и <CED, если известно, что <AOB – развернутый, <CED – не развернутый < CED < < AOB Задача 13.07.2012 8 www.konspekturoka.ru |
| Слайд №9 | |
 |
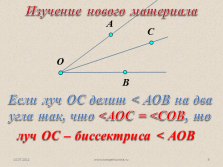
13.07.2012 www.konspekturoka.ru 9 Если луч ОС делит < АОВ на два угла так, что <АОС = <СОВ, то луч ОС – биссектриса < АОВ Изучение нового материала |
| Слайд №10 | |
 |
А В О Б и с с е к т р и с а Построение биссектрисы угла 13.07.2012 10 www.konspekturoka.ru |
| Слайд №11 | |
 |
А В О Б и с с е к т р и с а Построение биссектрисы угла 13.07.2012 11 www.konspekturoka.ru |
| Слайд №12 | |
 |
D R О Разделите угол на три равные части 13.07.2012 12 www.konspekturoka.ru |
| Слайд №13 | |
 |
13.07.2012 13 Викторина! 1. Единица измерения углов. (Градус) 2. Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле. (Градусная мера угла) 6. Градусная мера развернутого угла. (Градус) 4. 1/60 часть градуса. (Минута) 5. 1/60 часть минуты. (Секунда) 3. 1/180 часть развернутого угла. (180°) 7. Градусная мера прямого угла. (90°) 8. Градусная мера не развернутого угла. (меньше 180°) 9. Угол, градусная мера которого меньше прямого угла. (Острый) 9. Угол, градусная мера которого больше 90°, но меньше 180°. (Тупой) www.konspekturoka.ru |
| Слайд №14 | |
 |
13.07.2012 www.konspekturoka.ru 14 Свойства углов: 1. Равные углы имеют равные градусные меры. 2. Меньший угол имеет меньшую градусную меру. 3. Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов. |
| Слайд №15 | |
 |
13.07.2012 www.konspekturoka.ru 15 Решение Задача |
| Слайд №16 | |
 |
13.07.2012 www.konspekturoka.ru 16 Задача Луч ОС делит угол AOВ на два угла. Решение < AOC – на 15° больше < COB, значит < AOC = < COB + 15° <AOB = < AOC + <COB = 155°, тогда <COB + <COB + 15° = 155° <COB + <COB = 155° — 15° <COB + <COB = 140°, <COB = 70° < AOC = 70° + 15° = 85° Ответ: < AOC = 85° |
| Слайд №17 | |
 |
13.07.2012 www.konspekturoka.ru 17 Задача < AOD прямой, < АOB = <BOC = <COD Угол образованный биссектрисами < АOB и <COD? Решение Так как <AOD прямой, то <АOB = <BOC = <COD = 30° Пусть ОМ – биссектриса < АOB, ON – биссектриса <COD. <MOB = 15° и <CON = 15°, a <BOC = 30° <MON = <MOB + <CON + <BOC = 15° + 15° + 30° = 60° Ответ: < MON = 60° |
| Слайд №18 | |
 |
13.07.2012 18 Ответить на вопросы: Какие геометрические фигуры называются равными? Что такое угол? Какой угол называем развернутым? В каком случае будут равны углы? Что называется биссектрисой угла? Как ее построить? Назвать свойства углов. Назвать единицы измерения углов? Какие виды углов вы знаете? www.konspekturoka.ru |
