Вписанный угол
Скачать презентацию (0.03 мб)
Слайды и текст этой презентации
| Слайд №1 | |
 |
Вписанный угол |
| Слайд №2 | |
 |
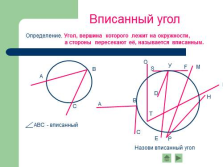Определение. Угол, вершина которого лежит на окружности, а стороны пересекают её, называется вписанным. Вписанный угол |
| Слайд №3 | |
 |
Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 1 случай. ВС проходит через центр окружности. Проведём ОА. Тогда дуга АС меньше полуокружности. |
| Слайд №4 | |
 |
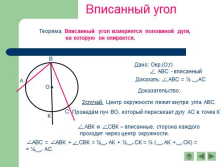Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 2случай. Центр окружности лежит внутри угла АВС. Проведём луч ВО, который пересекает дугу АС в точке К |
| Слайд №5 | |
 |
Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Доказательство: 3 случай. Центр окружности лежит вне угла АВС. Проведём луч ВО, который пересекает Oкр(О;r) в точке К |
| Слайд №6 | |
 |
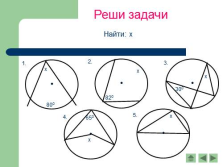Реши задачи Найти: х |
| Слайд №7 | |
 |
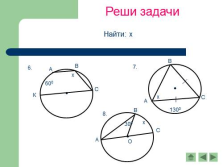Реши задачи Найти: х |
| Слайд №8 | |
 |
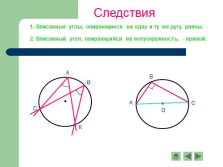Следствия 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны. 2. Вписанный угол, опирающийся на полуокружность, — прямой. |
| Слайд №9 | |
 |
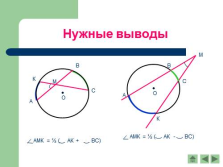Нужные выводы |
| Слайд №10 | |
 |
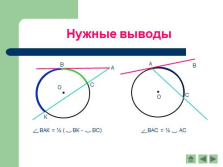
О С Нужные выводы |
| Слайд №11 | |
 |
Свойство пересекающихся хорд Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Дано: Окр.(О;r) М – точка пересечения хорд АВ и СК Доказательство: |
| Слайд №12 | |
 |
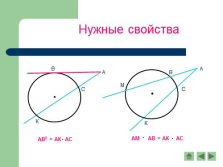Нужные свойства |
| Слайд №13 | |
 |
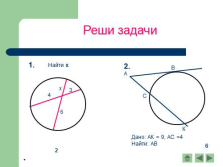Реши задачи 2 С 6 |
| Слайд №14 | |
 |
Желаю успехов в учёбе Михайлова Л. П. ГОУ ЦО № 173. |
