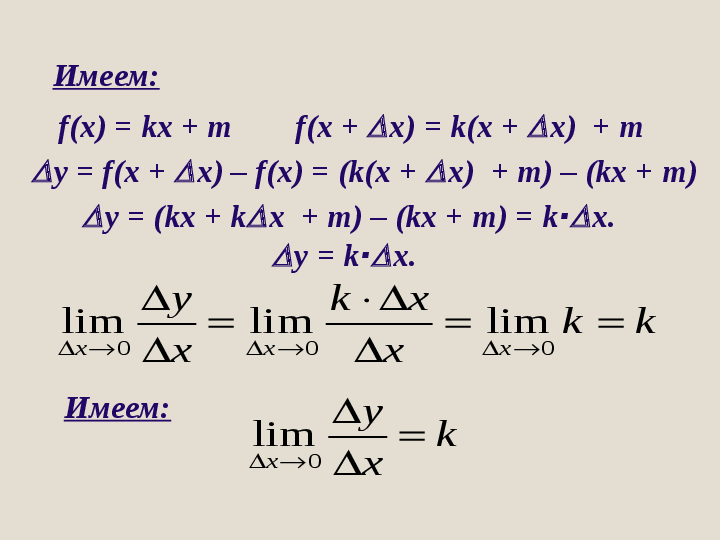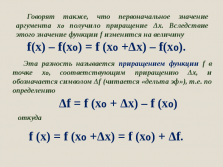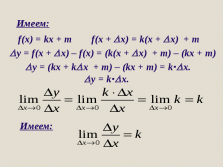Презентация приращение функции, 10 класс

Приращение аргумента.
Приращение функции.МБОУ лицей №10 города Советска
Калининградской области
учитель математики
Разыграева Татьяна Николаевна

При сравнении значения функции f в некоторой фиксированной точке x₀ со значениями этой функции в различных точках x, лежащих в окрестности x₀, удобно выражать разность f(x) – f(x₀) через разность x – x₀, пользуясь понятиями «приращение аргумента» и «приращение функции».Пусть x – произвольная точка, лежащая в некоторой окрестности фиксированной точки x₀. Разность x – x₀ называется приращением независимой переменной ( или приращением аргумента) в точке x₀ и обозначается Δx. Таким образом,

Δx = x –x₀

откуда следует, что

x = x₀ + Δx.

Говорят также, что первоначальное значение аргумента x₀ получило приращение Δx. Вследствие этого значение функции f изменится на величину
f(x) – f(x₀) = f (x₀ +Δx) – f(x₀).Эта разность называется приращением функции f в точке x₀, соответствующим приращению Δx, и обозначается символом Δf (читается «дельта эф»), т.е. по определению

Δf = f (x₀ + Δx) – f (x₀)

откуда
f (x) = f (x₀ +Δx) = f (x₀) + Δf.

При фиксированном x₀ приращение Δf есть функция от Δx. Δf называют также приращением зависимой переменной и обозначают через Δy для функции y = f(x) .Пример №1.

Найти приращение функции функции у = х² при
переходе от точки х₀ = 1 к точкам : а) х = 1,1; б) х = 0,98

Решение:

а) f(1) = 1² = 1; f(1,1) = 1,1² = 1,21;
 y = f(1,1) — f(1) = 1,21 – 1 = 0,21

Δy= f (x₀ + Δx) – f (x₀)

б) f(1) = 1; f(0,98) = 0,98² = 0,9604;
 y = f(0,98) — f(1) = 0,9604 – 1 = — 0,0396.

Функция y = f(x) непрерывна в точке
х = а, если в точке х = а выполняется
следующее условие:
если  х  0, то  у  0.Пример № 2.

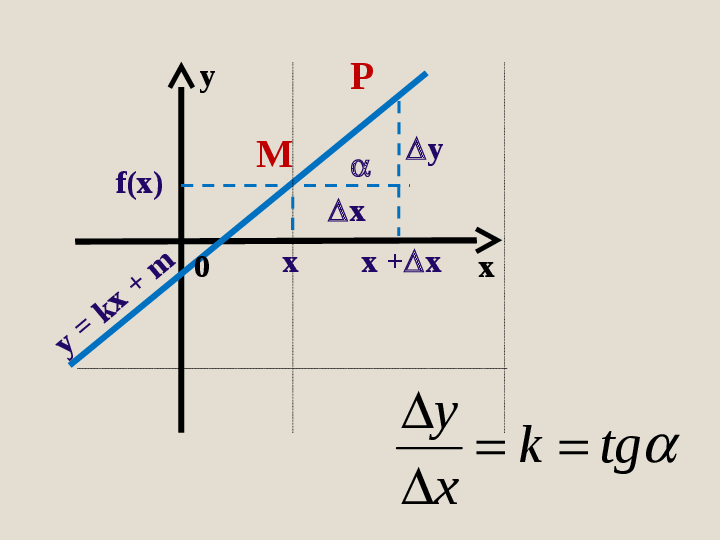
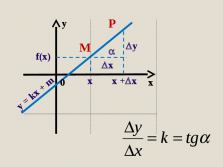
Для функции y = kx + m найти: а) приращение функции
при переходе от фиксированной точки х к точке х +  х;
б) предел отношения приращения функции к приращению
аргумента, при условии, что приращение аргумента
стремится к нулю.

Решение.

Имеем:f(x) = kx + m

f(x + x) = k(x + x) + m

y = f(x + x) – f(x) = (k(x + x) + m) – (kx + m)

y = (kx + kx + m) – (kx + m) = k·x.

y = k·x.

Имеем:

Mx

y = kx + m

x

f(x)

y

P

x +x

y

0

x



Пример № 3.Для функции y = x² найти: а) приращение функции
при переходе от фиксированной точки х к точке х +  х;
б) предел отношения приращения функции к приращению
аргумента, при условии, что приращение аргумента
стремится к нулю.

Решение.

Имеем:

f(x) = x²

f(x + x) = (x + x)²

y = f(x + x) – f(x) = (x + x)² — x² =
= (x² + 2xx + (x)²) — x² = 2xx + (x)².

Получили:y = 2xx + (x)².

Итак, для заданной функции y = x² получили: