Решение тригонометрических уравнений

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙУчитель: Копеина
Наталья Васильевна
10 класс
МОУ «Киришский лицей»

Содержание.Вводная часть, повторение теоретического материала.
Решение тригонометрических уравнений.
Проблемы, возникающие при решении тригонометрических уравнений.

ЦЕЛЬ:Повторить решение тригонометрических
уравнений.
1. Знать формулы для решения простейших тригонометрических уравнений.
2. Различать типы тригонометрических уравнений и знать способы их решений.
3. Уметь решать тригонометрические уравнения любых типов.
Выделение основных проблем при решении
этих уравнений:
Потеря корней.
Посторонние корни.
Отбор корней.

Устная работа.Решите уравнения
А) 3 х – 5 = 7
Б) х2 – 8 х + 15 = 0
В) 4 х2 – 4 х + 1= 0
Г) х4 – 5 х2 + 4 = 0
Д) 3 х2 – 12 = 0Ответы
4
3; 5
0,5
-2; -1; 1; 2
-2; 2

Устная работаУпростите выражения
А) (sin a – 1) (sin a + 1)
Б) sin2 a – 1 + cos2 a
В) sin2 a + tg a ctg a + cos2 a
Г)Ответы
— cos2 a
0
2
|1- tg х|

Повторим значения синуса и косинусау π/2 90°
1
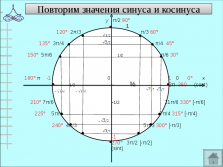
120° 2π/3 π/3 60°135° 3π/4 π/4 45°150° 5π/6 1/2 π/6 30°
180° π -1 0 1 0 0° x
-1/2 ½ 2π 360 (cost)

210° 7π/6 -1/2 11π/6 330° [-π/6]
225° 5π/4 7π/4 315° [-π/4]

240° 4π/3 5π/3 300° [-π/3]
-1
270° 3π/2 [-π/2]
(sint)

Арккосинусухπ/2

0

π

1

-1

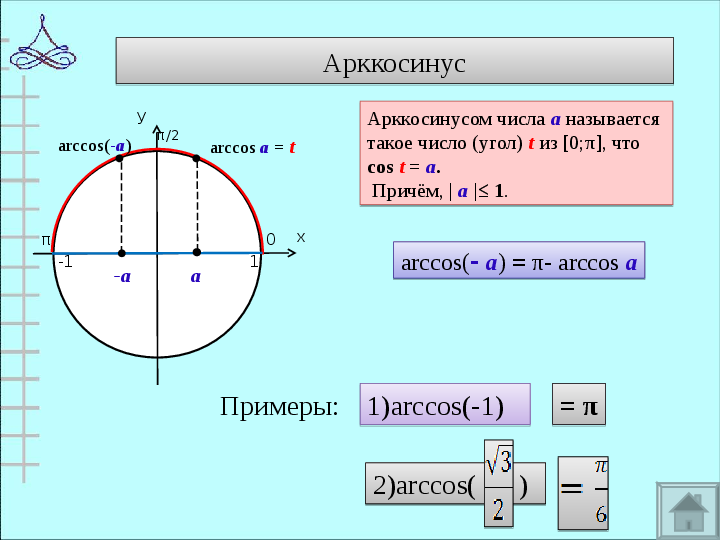
-а

а

arccos а = t

arccos(-а)

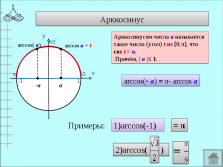
Арккосинусом числа а называется
такое число (угол) t из [0;π], что
cos t = а.
Причём, | а |≤ 1.

arccos(- а) = π- arccos а

Примеры:

1)arccos(-1)

= π

2)arccos( )

АрксинусПримеры:ух

π/2

-π/2

-1

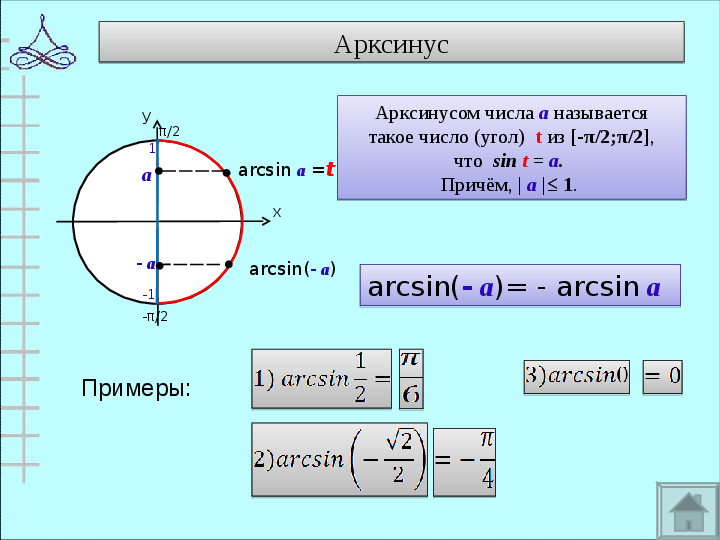
1

а

arcsin а =t

— а

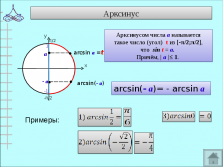
arcsin(- а)= — arcsin а

arcsin(- а)

Арксинусом числа а называется
такое число (угол) t из [-π/2;π/2],
что sin t = а.
Причём, | а |≤ 1.

Арктангенсуπ/2-π/2

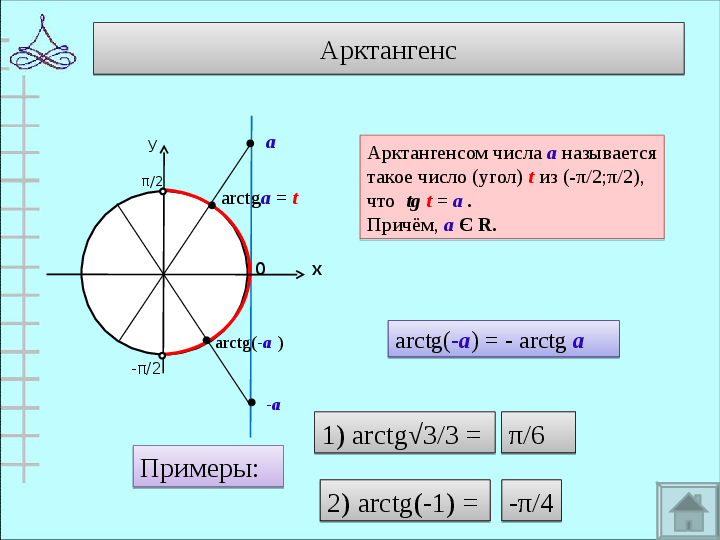
х

0

а

arctgа = t

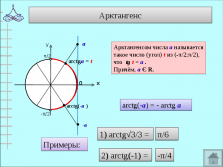
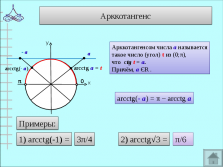
Арктангенсом числа а называется
такое число (угол) t из (-π/2;π/2),
что tg t = а .
Причём, а Є R.

arctg(-а) = — arctg а

-а

arctg(-а )

Примеры:

1) arctg√3/3 =

π/6

2) arctg(-1) =

-π/4

Арккотангенсух0

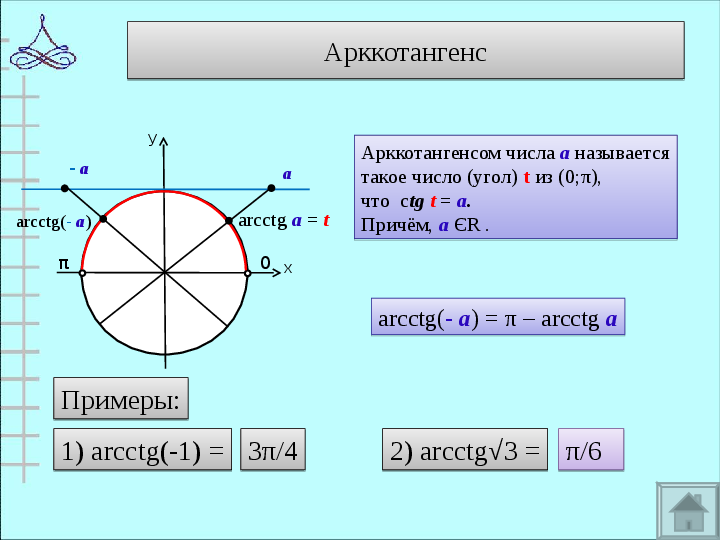
π

а

arcctg а = t

Арккотангенсом числа а называется
такое число (угол) t из (0;π),
что ctg t = а.
Причём, а ЄR .

arcctg(- а) = π – arcctg а

— а

arcctg(- а)

1) arcctg(-1) =

Примеры:

3π/4

2) arcctg√3 =

π/6

Повторение1 вариант
sin (-π/3)
cos 2π/3
tg π/6
ctg π/4
cos (-π/6)
sin 3π/4
arcsin √2/2
arccos 1
arcsin (- 1/2 )
arccos (- √3/2)
arctg √32 вариант
cos (-π/4 )
sin π/3
ctg π/6
tg π/4
sin (-π/6)
cos 5π/6
arccos √2/2
arcsin 1
arccos (- 1/2)
arcsin (- √3/2)
arctg √3/3

ПовторениеОтветы 1 вариант
— √3/2
— 1/2
√3/3
1
√3/2
√2/2
π/4
0
— π/6
5π/6
π/3Ответы 2 вариант
√2/2
√3/2
√3
1
— 1/2
— √3/2
π/4
π/2
2π/3
— π/3
π/6

Формулы корней простейших тригонометрических уравнений1.cost = а , где |а| ≤ 1илиЧастные случаи

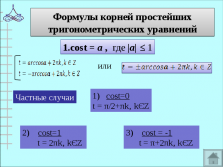
1) cost=0
t = π/2+πk‚ kЄZ

2) cost=1
t = 2πk‚ kЄZ

3) cost = -1
t = π+2πk‚ kЄZ

Формулы корней простейших тригонометрических уравнений2. sint = а, где | а |≤ 1илиЧастные случаи

1) sint=0
t = πk‚ kЄZ

2) sint=1
t = π/2+2πk‚ kЄZ

3) sint = — 1
t = — π/2+2πk‚ kЄZ

Формулы корней простейших тригонометрических уравнений3. tgt = а, аЄRt = arctg а + πk‚ k ЄZ4. ctgt = а, а ЄR

t = arcctg а + πk‚ kЄZ

При каких значениях х имеет смысл выражение:1.arcsin(2x+1)2.arccos(5-2x)3.arccos(x²-1)

4.arcsin(4x²-3x)

1) -1≤ 2х+1 ≤1
-2≤ 2х ≤0
-1≤ х ≤0
Ответ: [-1;0]

2) -1≤ 5-2х ≤1
-6≤ -2х ≤ -4
2≤ х ≤3
Ответ: [2;3]

-1≤ х²-1 ≤ 1
0 ≤ х² ≤2
Ответ:

Примеры:cost= — ;2) sint = 0;3) tgt = 1;

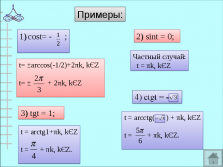
t= ±arccos(-1/2)+2πk, kЄZ
t= ± + 2πk, kЄZ

Частный случай:
t = πk, kЄZ

t = arctg1+πk, kЄZ
t = + πk, kЄZ.

t = arcctg( ) + πk, kЄZ
t = + πk, kЄZ.

Решение простейших уравненийtg2x = -12x = arctg (-1) + πk, kЄZ
2x = -π/4 + πk, kЄZ
x = -π/8 + πk/2, kЄZ
Ответ: -π/8 + πk/2, kЄZ.2) cos(x+π/3) = ½
x+π/3 = ±arccos1/2 + 2πk, kЄZ
x+π/3 = ±π/3 + 2πk, kЄZ
x = -π/3 ± π/3 + 2πk, kЄZ
Ответ: -π/3 ± π/3 + 2πk, kЄZ

3) sin(π – x/3) = 0
упростим по формулам приведения
sin(x/3) = 0
частный случай
x/3 = πk, kЄZ
x = 3πk, kЄZ.
Ответ: 3πk, kЄZ.

Виды тригонометрических уравнений1.Сводимые к квадратным
Решаются методом введения новой переменной
a∙sin²x + b∙sinx + c=0
Пусть sinx = p, где |p| ≤1, тогда a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и решить простые уравнения.

Виды тригонометрических уравнений2.Однородные
1)Первой степени:
Решаются делением на cos х (или sinx) и методом введения новой переменной.
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно не равны нулю, то разделим обе части уравнения на cosx (или на sinx). Получим: простое уравнение
a∙tgx + b = 0 или tgx = mПример. Решите уравнение sinx + 2cosx = 0.
Решение: Разделим обе части уравнения на cosx.Получим
Ответ:

Виды тригонометрических уравнений2) Однородные уравнения второй степени:
Решаются делением на cos² х (или sin²x) и методом введения новой переменной.
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x. Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.П р и м е р .   Решить уравнение:  3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.Р е ш е н и е .  3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tg2 x + 4 tg x + 3 = 0 ,  отсюда  y 2 + 4y +3 = 0 ,

корни этого уравнения:  y1 = 1,  y2 = 3,  отсюда
1)   tg x = –1,  2)   tg x = –3,
Ответ:

Виды тригонометрических уравнений3. Уравнение вида:
А sinx + B cosx = C. А, В, С  0sin x + cos x = 1 .
Р е ш е н и е .   Перенесём все члены уравнения
влево:
sin x + cos x – 1 = 0 ,

Виды тригонометрических уравнений4. Решение тригонометрических уравнений с помощью универсальной
тригонометрической подстановки
Решаются с помощью введения вспомогательного аргумента.А sinx + B cosx = CПри переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения  корнями данного уровнения.

Проверка
Если ,
— не верно, значит
, не является корнями исходного уравнения
Ответ:

Формулы.a cosx +b sinx заменим на C sin(x+), гдеsin =cos =

 — вспомогательный аргумент.

Универсальная подстановка.

х   + 2n; Проверка обязательна!

Понижение степени.
= (1 + cos2x ) : 2
= (1 – cos 2x) : 2

Метод вспомогательного аргумента.

Правила.Увидел квадрат – понижай степень.
Увидел произведение – делай сумму.
Увидел сумму – делай произведение.

1.Потеря корней:делим на g(х).
опасные формулы (универсальная подстановка).Этими операциями мы сужаем область определения.
2. Лишние корни:возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.

Потеря корней, лишние корни.

Решение тригонометрических уравнений по известным алгоритмамВариант 1.
На «3»
3 sin x+ 5 cos x = 0
5 sin2 х — 3 sinх cos х — 2 cos2х =0
На «4»
3 cos2х + 2 sin х cos х =0
5 sin2 х + 2 sinх cos х — cos2х =1
На «5»
2 sin x — 5 cos x = 3
1- 4 sin 2x + 6 cos2х = 0Вариант 2.
На «3»
cos x+ 3 sin x = 0
6 sin2 х — 5 sinх cos х + cos2х =0
На «4»
2 sin2 x – sin x cosx =0
4 sin2 х — 2sinх cos х – 4 cos2х =1
На «5»
2 sin x — 3 cos x = 4
2 sin2 х — 2sin 2х +1 =0